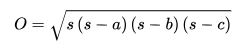Had Hero van Alexandrië – hij wordt ook wel Heron of soms Heroon genoemd – vandaag de dag geleefd, dan zou hij waarschijnlijk als illusionist de mensen vermaken en verbazen met trucs, waarbij hij dankbaar gebruik zou maken van zijn wetenschappelijke kennis. Eigenlijk deed deze wiskundige en technicus dit 2000 jaar geleden namelijk ook al. Zo is hij degene die er voor zorgt dat niet priesters maar de goden zelf de deuren van een tempel openen, kan hij water in wijn laten veranderen – waar hebben we dat eerder gelezen – en laat hij een fontein “eeuwig” stromen.
Hero is ook bekend als wetenschapper. Zo bedenkt hij een wiskundige formule om de oppervlakte van een driehoek te berekenen zonder gebruik te maken van een loodlijn (dat is de hoogte van de driehoek). Zijn methode maakt alleen gebruik van de lengtes van de drie zijdes, een methode die door landmeters vandaag de dag nog steeds veelvuldig wordt gebruikt. Ook construeert hij een hodometer. Dat is een apparaat waarmee men de afgelegde afstand van een voertuig kan berekenen, een soort voorloper van de kilometerteller van auto’s. En alsof dat nog niet genoeg is, had hij met één van zijn uitvindingen er ook nog bijna voor gezorgd dat de industriële revolutie al in de eerste eeuw na Christus was begonnen. Ook bedenkt hij een frisdranken-automaat avant la lettre.
Hero van Alexandrië
Veel is er over de persoon Hero van Alexandrië niet bekend. Een tijd lang heeft men zelfs gedacht dat hij zo’n 150 jaar voor Christus leefde en niet in de eerste eeuw na Christus, maar in één van zijn geschriften vermeldt hij een zonsverduistering die te herleiden is naar een zonsverduistering in het jaar 62 na Christus. Op grond daarvan wordt tegenwoordig meestal het jaar 10 na Christus als zijn geboortejaar genoemd en het jaar 70 als het jaar waarin hij overlijdt. Maar deze jaartallen zijn vrij arbitrair. We weten dat hij een Griek is, maar waar hij geboren is en onder welke omstandigheden is onbekend.
Hero zoals hij staat afgebeeld in de Codex of Saint Gregory Nazianzenos, een Grieks boek uit de negende eeuw. De kans is erg groot dat dit portret, net zoals bij veel portretten van wetenschappers uit het verleden, volledig ontsproten is uit de fantasie van de illustrator.
We weten wel – zie zijn naam – waar hij woont en werkt: Alexandrië. Deze Egyptisch stad, vernoemd naar Alexander de Grote, telt in de eerste eeuw na Christus naar verluidt zo’n 400.000 inwoners en is daarmee na Rome de grootste stad van het Romeinse rijk. Beroemd is de stad dankzij zijn bibliotheek en het is ook hier waar Hero van Alexandrië vaak werkt. Hij geeft er les in het Mouseion van Alexandrië.
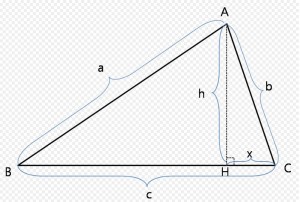
Hero van Alexandrië staat vandaag de dag vooral bekend als bedenker van allerlei wonderlijke apparaten, maar hij was in de eerste plaats wetenschapper. Zo bedenkt hij een methode om de oppervlakte van een driehoek te berekenen zonder gebruik te maken van een loodlijn. Dit werkt als volgt. Stel we hebben de volgende driehoek (met de punten A, B en C met als lengte van de drie zijdes: a, b, en c.
De Lijn AH is de zogenaamde loodlijn die de hoogte van de driehoek aangeeft. Deze lijn, start in een hoekpunt en eindigt loodrecht op de tegenovergestelde zijde. De oppervlakte O van de driehoek is nu gelijk aan O = ½ * h * c, waarbij h de lengte van de loodlijn is en c de lengte is van de zijde van de driehoek waar de loodlijn op eindigt.
Nu is het probleem waar landmeters vaak tegen aanlopen dat ze wel goed de afstanden tussen de vaste punten A, B en C (daar staan de paaltjes in het veld) kunnen meten, maar dat de exacte locatie van het punt H – daar staat geen paaltje – in de praktijk lastig valt te bepalen. Daarmee is ook het meten van de lengte van de loodlijn ‘h’ lastig.
Hier is een wat overijverige landmeter aan het werk geweest. foto: Notjake13
Hero bedacht hier oplossing voor. Hij kwam met een andere formule om de oppervlakte van een driehoek te berekenen en wel eentje die alleen gebruik maakte van de lengtes van de drie zijdes van de driehoek. Zijn formule luidde:
Hierbij geldt s = (a + b + c) / 2 (oftewel de helft van de omtrek van de driehoek). Dit is een wat ingewikkelder formule om de oppervlakte van de driehoek te berekenen, maar je hoeft niet de lengte van de loodlijn h te weten. Wel moet je worteltrekken en dat kan lastig kan zijn als O niet gelijk is aan een kwadraat van een geheel getal.
Voor dit probleem formuleert Hero echter een simpel algoritme. Stel je wilt bijvoorbeeld de wortel trekken van het getal 130. Tegenwoordig type je dit getal in op een rekenmachinetje dat je bij een zak winterpenen hebt gekregen, drukt op een knop met een wortelteken en je ziet dat de uitkomst van de wortel van 130 afgerond 11,40 is. Vroeger was het echter een heel gedoe om een wortel te trekken totdat Hero het volgende truckje (algoritme) bedacht (zet u schrap, we gaan even rekenen):
- Stap 1: Begin met een getal waarvan het kwadraat bij voorkeur zo dicht mogelijk bij 130 ligt (dat scheelt in het aantal keer dat je het stappenplan moet doorlopen). In dit geval nemen we 11. (11² = 121).
- Stap 2: deel 130 door 11. Dit geeft 11,82 als uitkomst.
- Stap 3: tel dit getal op bij het getal waarmee je deelde (11) en deel de uitkomst van deze som door 2: Dit geeft (11 + 11,82) / 2 = 11,41. Je ziet, je zit al heel dicht bij de uiteindelijke uitkomst van 11,40 (voorkennis). Vervolgens herhaal je de stappen 2 en 3 met de gevonden tussenuitkomsten net zolang tot de uitkomsten van stap 2 en stap 3 gelijk aan elkaar zijn
- Stap 2 dus opnieuw: 130 nu gedeeld door 11,41. Dit geeft 130 / 11,41 = 11,39;
- Stap 3 opnieuw: (11,41 + 11,39) / 2 = 11,40. De getallen 11,39 en 11,40 zijn al bijna aan elkaar gelijk. We herhalen het proces nog één keertje.
- Stap 2 opnieuw: nu 130 gedeeld door 11,40. Dit geeft 130 / 11,40 = 11,40. Deze uitkomst is gelijk aan de deler en de wortel van 130 is dus 11,40. (Wisten we al; even ter controle: 11,40 x 11,40 = 130; mooi, het algoritme werkt.)
Het aantal keer dat je deze stappen moet doorlopen hangt af van de vraag hoeveel cijfers nauwkeurig je achter de komma wilt hebben en van het getal waarmee men het iteratieproces begint. Stel je was niet met het getal 11 maar met het getal 25 begonnen – dit omdat je om de een of andere reden dacht dat het kwadraat van 25 in de buurt van 130 zou liggen. (Goed fout; in werkelijkheid is het kwadraat van 25 gelijk aan 625.) Het algoritme – “herhaling is de kracht van de reclame”- werkt echter nog steeds. Alleen moeten we nu negen keer in plaats van zes keer aan het werk.
Als u gelooft dat ik het rekenwerk goed heb gedaan, dan kunt u de volgende berekeningen gerust overslaan, zo niet, zie dan hier:
- Stap 2: deel 130 nu door 25. Dit geeft 5,2 als uitkomst.
- Stap 3: tel dit getal op bij het getal waarmee je deelde (25) en deel de uitkomst van deze som door 2: Dit geeft (25 + 5,2 )/ 2 = 15,1.
- Stap 2 weer: deel 130 nu door 15,1, dat geeft 130 / 15,1 = 8,61;
- Stap 3 opnieuw: (15,1 + 8,61) / 2 = 11,85
- Weer een keertje stap 2 (we blijven bezig). Nu delen we door 11,85. Dit geeft 130 / 11,85 = 10,97
- En dan stap 3 weer: (11,87 + 10,97) / 2 = 11,41
- Stap 2 weer (zucht): 130 / 11,41 = 11,39
- En dan nog een keertje stap 3 (11,41 + 11.39) / 2 = 11,40
- En – hè, hè, voor de laatste keer – stap 2: 130 gedeeld door 11,40 = 11,40. De uitkomst is eindelijk gelijk aan de deler en de wortel van 130 is dus 11,40.)
Als je in het begin met een te groot of te klein getal begint, moet je het stappenplan wat vaker doorlopen, maar je komt er uiteindelijk wel. Overigens hoef je niet persé met een geheel getal te beginnen. Als je denkt dat de wortel van 130 ergens ligt tussen de 11 en 12 dan kan je ook met een getal beginnen dat tussen deze twee getallen in ligt. En kies je toevallig 11,40 als eerste deler, dan ben je zelfs in één keer klaar! Enfin, u kunt nu ook worteltrekken. Vraag niet hoe het kan maar profiteer ervan.
Hero van Alexandrië is niet de eerste die met deze methode van worteltrekken op de proppen komt. Ook de oude Grieken en de Chinezen kennen deze methode al. Maar wel is Hero de eerste die deze methode uitgebreid beschrijft. Hij doet dit in zijn boek ‘Metrica’, een uit drie delen bestaand werk waarin hij over allerlei wiskundige zaken schrijft, onder andere over het berekenen van de oppervlakte van driehoeken, vierhoeken en regelmatige veelhoeken. Ook beschrijft hij hierin hoe je het volume van bollen, cilinders, kegels, prisma’s en piramides kan uitrekenen. Hij maakt hierbij gebruik van het werk van Archimedes, wiens naam Hero dan ook met ere in het voorwoord vermeldt.
Zijn de meeste wetenschappers van tegenwoordig specialisten op één vakgebied, Hero is net zoals de meest wetenschappers uit de oudheid thuis in meerdere vakgebieden. Zo houdt hij zich naast de wiskunde ook bezig met natuurkunde, astronomie, landmeetkunde, mechanica en de theorie van het licht. Zo beschrijft hij in één van zijn werken hoe je de afstand tussen Rome en Alexandrië kan berekenen door te kijken naar het tijdverschil tussen de waarnemingen in Rome en Alexandrië van dezelfde maansverduistering.
Hero van Alexandrië wordt genoemd als de schrijver van vijftien boeken. Van zeven boeken is het zeker dat hij deze heeft geschreven, van de andere acht niet helemaal. In de tijd van voor de boekdrukkunst – als de boeken nog met de hand worden overgeschreven – is het vaak zo dat in wetenschappelijke werken de nieuwste inzichten bij het overschrijven van de oude boeken worden meegenomen en dat verouderde inzichten worden verwijderd. Hierdoor is het van een boek niet altijd meer duidelijk is wie nou wat heeft geschreven.
Behalve de Metrica is Hero’s naam in elk geval verbonden met boeken over mechanica, hydraulica, het meten van afstanden en hoe het licht zich in vloeistoffen voortplant. Het beroemdst zijn echter Hero’s boeken ‘Pneumatica’ en ‘Automata’. In deze twee boeken beschrijft hij allemaal ingenieuze machines die hij heeft bedacht.
De voorkant van een Italiaanse heruitgave van de ‘Automata’ uit 1589 ,
Een aantal machines van Hero zorgt in zijn tijd voor grote verbazing bij de toeschouwers. Beroemd zijn de automatisch openende tempeldeuren. Voor een gesloten tempeldeur steken de priesters een vuur aan. Als er door de toeschouwers voldoende is geofferd en de goden tevreden zijn – lees de priesters – dan openen de goden de deuren zonder hulp van de mens. Althans zo wordt het de toeschouwers verteld. Wat ze niet weten, is dat onder de vuurkorf en de tempel zich een buizenstelsel met water bevindt. Het water wordt door het vuur verwarmd en loopt daardoor over in een andere vat en met behulp van gewichten en een katrol openen de deuren daarna “uit zichzelf”. Het is echter geen werk van de goden. Het is de wetenschap.
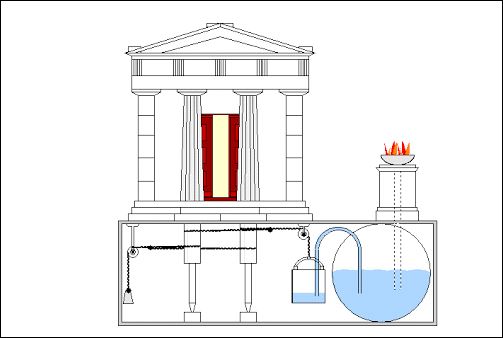 Tekening die laat zien hoe de tempeldeuren “automatisch kunnen openen”, Het vuur verwarmt het water. Daardoor stroomt er via een buis water in een emmer die aan een katrol hangt. Als er voldoende water in de emmer zit, zorgt het gewicht er voor dat de emmer zakt en draaien de tempeldeuren – “Ooh” en “Aah” roepen de toeschouwers – langzaam open. Tekening afkomstig van een blogpost van Jacqueline Febres; Peru 2010
Tekening die laat zien hoe de tempeldeuren “automatisch kunnen openen”, Het vuur verwarmt het water. Daardoor stroomt er via een buis water in een emmer die aan een katrol hangt. Als er voldoende water in de emmer zit, zorgt het gewicht er voor dat de emmer zakt en draaien de tempeldeuren – “Ooh” en “Aah” roepen de toeschouwers – langzaam open. Tekening afkomstig van een blogpost van Jacqueline Febres; Peru 2010
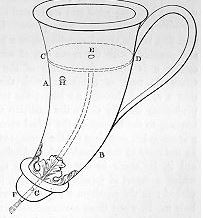
Een andere beroemde ‘uitvinding’ is de kruik die water in wijn laat veranderen.
Men vult de kruik met water. De kruik omvat echter al een compartiment met wijn. Ook bevat de kruik een aantal luchtopeningen. Als men nu bij het uitschenken bepaalde openingen van de kruik met zijn vingers bedekt, wordt het watercompartiment afgesloten en stroomt er wijn uit de kruik. De verbaasde toeschouwers denken dat ze water in wijn hebben zien veranderen. In de Bijbel staat in Johannes 2 ook een verhaal waar water in wijn verandert. Of dit op dezelfde wijze geschiedt als in de kruik van Hero is niet bekend, maar het zou best wel eens kunnen. Geloof niet elk wonder dat u ziet.
Ook bedenkt Hero een drankautomaat waar je munten in moet werpen, waarna je drinken krijgt, een soort frisdrankautomaat.
Deze automaat werkt als volg. Je gooit door een gleuf boven in de kan een muntje. Het muntje belandt op een hefboom. Die kantelt door het gewicht van het muntje, waarna er een klepje omhoog wordt getrokken, waardoor er uit een opening in de kan vloeistof naar buiten stroomt. Als het muntje vervolgens van de schuin staande helling afglijdt, dan keert de hefboom terug naar zijn originele horizontale stand en sluit de opening van de kan weer. Hero is met dit idee zijn tijd ver vooruit. Het zal meer dan 1500 jaar duren voordat er in Engeland kleine koperen machines in cafés verschijnen die tabak uitgeven als je er een muntje ingooit.
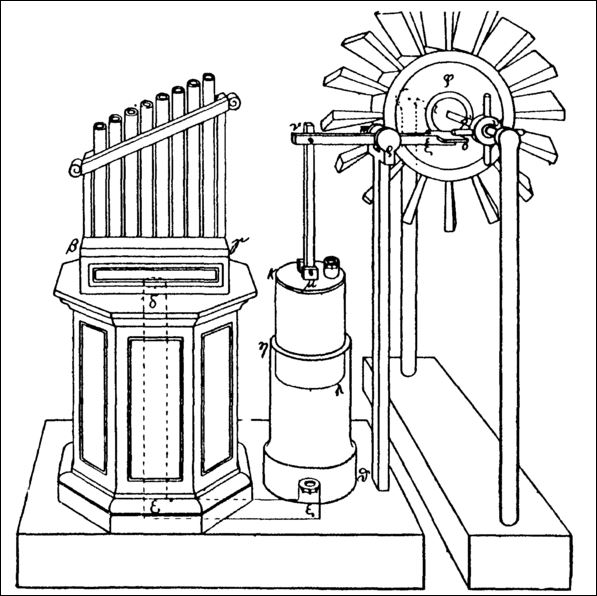
Ook ontwerpt Hero meerdere apparaten waarbij hij gebruik maakt van de windkracht. Zo construeert hij een windorgel dat muziek maakt dankzij een blaaspomp die beweegt met hulp van een windmolen.
Windorgel van Hero; tekening afkomstig uit W. Schmidt: Herons von Alexandria Druckwerke und Automatentheater, gr-dt, 1899
Hero heeft zoveel automaten bedacht dat er hier geen ruimte is om ze allemaal te beschrijven. Ook geldt dat een hoop apparaten van hem alleen op papier bestaan en in de praktijk nooit zouden kunnen functioneren, maar dat is een detail. Het blijven knap bedachte machines.
 Zie hier nog een paar schetsen van Hero. Ik heb overigens geen flauw idee waarvoor al deze machines zijn bedoeld.
Zie hier nog een paar schetsen van Hero. Ik heb overigens geen flauw idee waarvoor al deze machines zijn bedoeld.
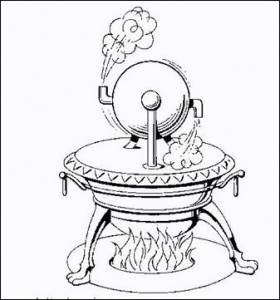
Van alle door Hero bedachte machines zijn twee apparaten later heel beroemd geworden. De eerste is de aeolipile, de tweede zijn hodometer. Met de aeolipile had Hero bijna de industriële revolutie zestien eeuwen eerder laten beginnen. Zijn aeolipile kunnen we namelijk zien als een soort stoommachine avant la lettre.
Links een ontwerptekening van de aeolipile; rechts een reconstructie van de aeolipile zoals deze te zien is in het Thessaloniki Technology Museum. Foto Gts-tg: Wikipedia
Het apparaat bestaat uit een vat met daarin water, een holle pijp die het vat met een bol verbindt, die om haar as kan ronddraaien. Aan deze bol zitten een tweetal uitlaten. Als men nu onder het vat een vuurtje stookt, dan wordt het water in het vat verwarmd. De ontstane hete stoom stijgt op naar de bol, waar de stoom vervolgens door de twee uitlaten met kracht naar buiten ontsnapt. Door de specifieke vorm en de plaats waar de uitlaten zitten, gaat de bol rond draaien. Aldus wordt energie omgezet in beweging. Zie hier het principe van de stoommachine die aan de basis staat van de industriële revolutie.
Alleen de laatste stap – het iets nuttig doen met die ronddraaiende beweging – die stap maken Hero en zijn landgenoten niet. Hadden ze dat wel gedaan, dan was wellicht de industriële revolutie al eeuwen eerder begonnen. Het apparaat van Hero wordt in zijn tijd vooral als een leuk speeltje gezien.
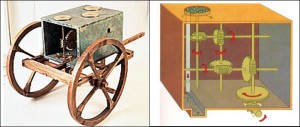
Tot slot: de hodometer, ook wel soms odometer genoemd. Hero beschrijft een dergelijk apparaat in hoofdstuk 34 van zijn boek ‘Dioptra’. De hodometer (het oud-Griekse woord hodos betekent ‘weg’) is een meetapparaat. Met behulp van een hodometer kan je de afstand die een voertuig heeft afgelegd berekenen.
Een reconstructie van Hero’s hodometer, Je kan het karretje achter een wagen hangen. Reconstructie gemaakt door het Thessaloniki Technology Museum; Rechts een schematische tekening van het mechanime
Het apparaat werkt met tandwielen waaraan een uitsteeksel zit. Elke keer als het wagenrad een omwenteling maakt, laat dit uitsteeksel een andere rad een stukje verder draaien. Dit rad laat op zijn beurt na een hele omwenteling weer een ander rad met een bakje draaien. Hierop liggen kiezelstenen. Als het rad een stukje is gedraaid, dan vallen de kiezelstenen er vanaf en komen dan in een soort vangbakje terecht.
Elke gevallen steen komt overeen met een bepaalde afgelegde afstand, die afhangt van de omtrek van de gebruikte wielraderen. In de tijd van Hero was de basiseenheid om een afstand te meten een Romeinse mijl; die had lengte van mile (duizend) passen. Dat stemt ongeveer overeen met 1478 meter. Door het aantal gevallen kiezelstenen in de mand te tellen, kan men de door de karrenwagen afgelegde afstand berekenen. Een kilometerteller van een auto werkt min of meer volgens hetzelfde principe, alleen maakt die gelukkig niet gebruik van vallende kiezelstenen.
Leonardo da Vinci heeft eeuwen later geprobeerd om op basis van de tekeningen van Vitruvius en Hero het apparaat na te bouwen, maar het lukte dit genie niet om een nauwkeurig werkend exemplaar te construeren. Het gaf te veel afwijkingen. De in 2018 op 93-jarige leeftijd overleden Nederlandse professor André Wegener Sleeswijk van de Universiteit van Groningen slaagt er in 1987 wel in om een goed werkend kopie van het ontwerp van Hero te bouwen. Hij maakt gebruik van tandwielen zoals deze zijn aangetroffen in het mechanisme van Antikythera in plaats van de tandwielen met pennen die Leonardo da Vinci gebruikt, wat doet vermoeden dat Hero wellicht ook op de hoogte was van de techniek die achter het mechanisme van Antikythera zit. Dit in tegenstelling tot Leonardo da Vinci.
Al met al kunnen we zeggen dat Hero van Alexandrië niet alleen een slimme wiskundige was, maar ook een groot technicus.
Hero is niet de eerste die het principe van een hodometer beschrijft. Naar verluidt had Archimedes – wie anders – ook al een soort hodometer bedacht. De eerste die een hodometer op papier beschrijft, is (hoogstwaarschijnlijk) de Romein Vitruvius, hij leeft in de eerste eeuw voor Christus. Maar het ontwerp van Hero is het bekendst geworden. Ook de Chinees Zhang Heng, hij leeft van 78 tot 139 na Christus, heeft onafhankelijk van Hero een soortgelijke hodometer ontworpen.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie