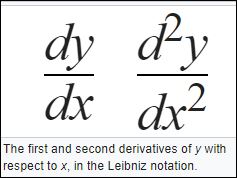Kent u die anekdote van de optimist en de pessimist die aan het discussiëren zijn over de wereld waarin wij leven? Op een gegeven zegt de optimist: “Volgens mij is de wereld waarin we leven de best mogelijke wereld die er kan bestaan”, waarop de pessimist antwoordt: “Ja, ik ben bang dat dit waar is.” Iemand die het optimistische standpunt uit zou kunnen dragen, zou Gottfried Leibniz geweest kunnen zijn. Met zijn filosofiepet op schreef hij namelijk eens dat we in de beste van alle mogelijk werelden leven.
Leibniz redeneerde ongeveer als volgt: ‘God zou van alle mogelijke werelden die er te scheppen zijn de beste scheppen. Als er een betere wereld denkbaar was, zou dat strijdig zijn met de alwetendheid van God. En als God een nog betere wereld niet gewild zou hebben, zou dat botsen met Gods goedheid. Kortom deze wereld waarin we leven inclusief alle negatieve zaken moet de best mogelijke wereld van alle werelden zijn.’ Letterlijk schrijft hij in 1714 zijn boek ‘Monadologie’: “Tout est pour le mieux dans le meilleur des mondes possibles” (“Alles is optimaal in de beste van alle mogelijke werelden.”).
Niet iedereen is het met Leibniz eens. Zo schrijft bijvoorbeeld Voltaire in 1749 een roman getiteld ‘Candide, ou l’optimisme’, waarin hij de hoofdpersoon, professor Pangloss, overduidelijk gebaseerd op Leibniz, allerlei tegenslagen laat ondervinden maar die steeds vrolijk ‘Alles gaat opperbest in het beste der werelden.’ blijft roepen.
Een Engelse uitgave van het boek van Voltaire uit 1762; Private Collection of S. Whitehead
Leibniz is niet alleen een filosoof maar ook een wiskundige, natuur-kundige, rechtsgeleerde, logicus en uitvinder, kortom een allround wetenschapper. Hij is vandaag de dag vooral bekend als de bedenker van de theorie van de differentiaal- en de integraalrekening.
Tegelijk met hem bedenkt in Engeland Isaac Newton ook de fundamenten van deze theorie. Dat leidt in het begin van de achttiende eeuw tot grote onenigheid tussen Engelse wetenschappers en die van continentaal Europa. De Engelsen stellen dat Newton, wiens theorie pas jaren na die van Leibniz wordt gepubliceerd maar die zijn gedachtegang al wel eerder in een brief aan Leibniz heeft beschreven – een brief die Leibniz naar eigen zeggen pas ontving nadat hij al zijn eigen theorie had bedacht en die hij ook nog eens direct had beantwoord – degene is die de theorie als eerste heeft bedacht en dat de vermaledijde Leibniz plagiaat heeft gepleegd. Deze ontkent dat vurig. Hij stelt dat hij zelf alles, geheel onafhankelijk van Newton, heeft bedacht.
In 1712 besluit de Engelse ‘Royal Society’, waar Newton op dat moment voorzitter van is – toeval – om een objectieve commissie in het leven te roepen die deze zaak voor eens en altijd moet uit zoeken. De geheel uit Engelsen bestaande commissie verzamelt allerlei stukken, die allemaal door een zeer behulpzame Newton worden aangeleverd; aan Leibniz wordt niets gevraagd . Op 24 april 1712 verschijnt de conclusie van de commissie. Newton is zo vriendelijk om de commissie te helpen bij het opstellen van de tekst.) De commissie wijst Newton aan als de oorspronkelijke bedenker van de theorie. Leibniz wordt weliswaar niet rechtstreeks van plagiaat beschuldigd, maar zijn fout is volgens de commissie wel een schending van de wetenschappelijke ethiek, zijnde het verbergen van het feit dat hij informatie heeft gebruikt die hem al bekend was.
Tegenwoordig is de heersende opvatting dat Newton en Leibniz beiden de theorie onafhankelijk van elkaar hebben bedacht. Newton tussen 1666 en 1669 (in 1671 schrijft hij twee concept-boeken over zijn theorie. Newton stuurt de concepten echter alleen maar naar een beperkte groep collega’s (niet naar Leibniz) en publiceert de boeken nog niet. Hij twijfelt namelijk of zijn theorie wel juist is en is bang dat zijn werken bekritiseerd zullen worden; het eerste van zijn twee boeken wordt pas in 1704 gepubliceerd en het tweede in 1736 – zijn tweede boek verschijnt pas negen jaar nadat Newton al is overleden.
Leibniz formuleert ergens in 1675 en 1676 zijn theorie (en doet dat onafhankelijk van Newton). Dat is weliswaarzo’n tien jaar later dan dat Newton dat deed, maar Leibniz publiceert zijn ontdekkingen wel veel eerder dan Newton. Leibniz publiceert namelijk zijn theorie al in 1684 – twintig jaar voor de verschijningsdatum van Newton’s eerste boek.
Leibnize doet dat in ‘Acta Eruditorum’, een wetenschappelijk tijdschrift dat hij zelf had opgericht. Het artikel draagt de eenvoudige titel ‘Nova Methodus pro Maximis et Minimis, itemque tangentibus, qua nec fractas, nec irrationales quantitates moratur, et singulare pro illi calculi genus’ . (Het betekent: Nieuwe methode voor maxima, minima, en raaklijnen die niet gehinderd wordt door breuken of irrationale grootheden en een bijzondere rekenmethode daarvoor.) In het artikel laar hij als voorbeeld zien dat je met zijn methode de formule kan afleiden voor de breking van licht. In 1686 verschijnt er nog een tweede publicatie van Leibniz over het onderwerp.
Newtons en Leibniz’ versies zijn conceptueel gezien iets verschillend. Die van Leibniz wordt algemeen als logischer gezien. Leibniz beschouwde een kromme lijn als de som van oneindig veel kleine lijnstukjes. Als je deze stukjes in steeds maar kleinere stukjes opdeelt, dan worden deze stukjes uiteindelijk oneindig klein: de zogenaamde differentialen, voorgesteld door het symbool ‘d’ (van differentia) en voor de som het symbool van deze stukjes bedacht hij het integraaltelen ‘ʃ’ dat een gotische s (van summa) voorstelt. De lengte van de kromme tussen twee punten is de som van deze oneindig kleine stukken. Leibniz is dan ook degene die voor differentieren en integreren de symbolen bedacht. Zie hier een pagina uit een artikel dat Leibniz schreef op 11 april 1675, waarin hij in de kantlijn rechts de symbolen noteert.
Newton introduceerde ook notaties voor differentieren, maar zijn notatie met puntjes op een x heeft veel minder navolging gekregen dan de notatie van Leibniz. Zie hier de twee notaties (voor een eerste en tweede differentatie) naast elkaar. Links die van Leibniz; rechts die van Newton.
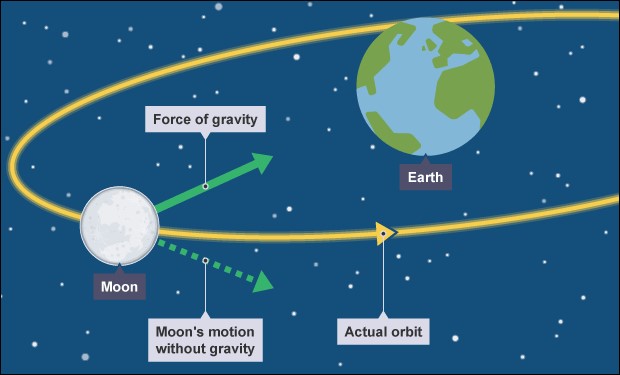
Het is overigens onduidelijk waarom Newton zo graag aangemerkt wil worden als de enige bedenker van de differentiaal- en de integraalrekening. Newton is namelijk op dat moment al wereldberoemd. Hij heeft de extra roem niet nodig. Hij is de man die – als hij tijdens een pestepidemie in 1667 thuis bij zijn ouders in quarantaine zit – een appel uit de boom ziet vallen en vervolgens de zwaartekracht uitvindt – herstel; begrijpt dat het de zwaartekracht van de aarde is die de maan gevangen houdt in een baan om de aarde.
(Even tussen haakjes: voor degene zich nu zorgen maakt en zich afvraagt waarom de maan niet, net zoals de appel op de aarde valt – immers de aarde trekt aan de maan en de maan iets minder hard aan de aarde (de aarde weegt 80 keer zo veel als de maan), dat komt omdat de maan tegelijkertijd met een snelheid van ongeveer 3680 km/uur door het heelal beweegt in een richting die loodrecht staat op de door de zwaartekracht veroorzaakte aantrekkingskracht richting aarde. De combinatie van deze twee zaken zorgt er voor dat de maan in een baan om de aarde blijft draaien en niet op de aarde ploft. Geen zorgen dus. Zie het hier uitgelegd in een (Engelstalig) plaatje.)
Newton is een briljante wetenschapper. Hij geldt met Blaise Pascal als de grootse geleerde uit deze periode, al zullen de Engelsen wel weer gaan roepen dat Newton de allergrootste is. Zo vormen de drie ‘wetten van Newton’ bijvoorbeeld de grondslag van de klassieke mechanica.
(Volgens zijn eerste wet, de traagheidswet, is een voorwerp waarop geen resulterende kracht werkt in rust of het beweegt zich rechtlijnig met constante snelheid voort. Volgens de tweede wet verandert een kracht de snelheid van een voorwerp en zijn derde wet stelt dat als een voorwerp A een kracht uitoefent op een voorwerp B deze kracht gepaard gaat met een even grote maar tegengestelde kracht van B op A. Deze derde wet staat ook wel bekend als ‘actie is reactie’ maar dat is strikt formeel gezien niet helemaal juist. Dat zou een tijdvolgorde inhouden (B reageert op A) en die tijdvolgorde is er niet, de krachten treden tegelijkertijd op.)
Newton had daarnaast ook nog eens baanbrekende ideeën op het gebied van de optica en warmteleer. Kortom roem genoeg vergaard zou je zeggen, maar blijkbaar wilde Newton ook graag gezien worden als de beste wiskundige van zijn tijd en kon hij het niet hebben dat iemand anders, (Leibniz) hetzelfde als hij bedenkt maar er eerder over publiceert.
Isaac Newton in 1689; schilderij van Sir Godfrey Kneller; collectie Institute for Mathematical Sciences, University of Cambridge; Newton kijkt een beetje alsof hij net gehoord heeft dat Leibniz eerder is met de publicatie van de theorie.
Wie is Leibniz
Leibniz als 49-jarige met een pruik op; schilderij van Christoph Bernhard Francke.
Gottfried Wilhelm Leibnütz – als hij twintig jaar oud is, verandert hij zijn achternaam in Leibniz – komt op zondag 1 juli 1646 om kwart voor zeven ’s avonds ter wereld in Leipzig. Dat van dat kwart voor zeven weten we dankzij het familieschrift waarin zijn vader het exacte tijdstip van de geboorte van Gottfried opschrijft. Niet dat het voor u en mij enig nut heeft om het tijdstip van zijn geboorte te weten (of de datum of het exacte geboortejaar), maar als zijn vader de moeite neemt om het op te schrijven, wie zijn wij dan om het hier ook niet te vermelden.
Vader Friedrich Leibnütz is hoogleraar moraalfilosofie – dat heeft iets met ethiek te maken – aan de Universiteit van Leipzig. Moeder Catharina Schmuck, een dochter van een rechtsgeleerde, is zijn derde vrouw. Zijn eerste twee echtgenotes zijn allebei jong gestorven. Van zijn tweede vrouw, dochter van een bibliothecaris, heeft Friedrich een grote collectie wetenschappelijke boeken geërfd en vlak voordat hij overlijdt – Gottfried is dan zes jaar oud – zegt hij dat de boeken voor Gottfried zijn. Zijn oudere halfbroer en halfzusje hebben er geen enkele belangstelling voor. Gottfried, zo jong als hij is, wel. Zijn vader heeft hem al vroeg leren lezen.
Probleem is wel dat de bibliotheek vooral bestaat uit in het Latijn geschreven wetenschappelijke boeken, maar naar eigen zeggen leert de jonge Gottfried zichzelf al op achtjarige leeftijd Latijn uit een geïllustreerd Livius-geschiedenisboek (Livius is een beroemd Romeins geschiedschrijver uit de tijd van keizer Augustus). Hoogstwaarschijnlijk moeten we dit verhaal echter met een grote korrel zout nemen (‘cum magno grano salis’).
Zijn moeder voedt hem Luthers op en stuurt Gottfried naar de protestante Nicolai-school in Leipzig. Daar leert hij niet alleen rekenen maar ook Latijn, Grieks, theologie en logica. Vooral dat laatste vak boeit hem erg. Op zijn veertiende gaat hij naar de universiteit van Leipzig. Dat klinkt vrij jong, maar het komt in die tijd wel vaker voor dat kinderen van die leeftijd naar de universiteit gaan. De eerste twee jaar van zijn universitaire studie betreffen een algemeen deel. Hij wordt onderwezen in vakken als wiskunde – dat staat in Leipzig in die tijd niet op een hoog niveau – filosofie, retorica en rechten. Ook krijgt hij les in verschillende talen (Engels, Frans, Latijn en Grieks.)
In 1663 haalt Leibniz er zijn ‘bachelorsdiploma’ met een proefschrift getiteld ‘De Principio Individui’, waarin hij (volgens de universiteit van St Andrews) benadrukt ‘dat de existentiële waarde van het individu, niet door materie alleen of alleen door vorm verklaard moet worden maar door zijn hele wezen.” (Ik vermoed dat u net als schrijver dezes deze zin twee keer heb moeten lezen en hem dan ook nog steeds niet begrijpt.)
Om zijn wiskundige kennis bij te spijkeren, volgt Gottfried in de zomer van 1663 in Jena een zomercursus wiskunde bij de bekende Duitse wiskundige en filosoof Erhard Weigel. Het is Weigel, die hem het belang van het bewijs in de wetenschap bij brengt. Weigel is ook de man die van mening is dat het getal niet alleen het fundament van de wiskunde vormt maar zelfs dat van het gehele universum. Zijn ideeën zullen een aanzienlijke invloed op Leibniz hebben, niet alleen op wiskundig gebied maar ook op het vlak van de filosofie en logica.
Gedenkplaat in Jena ter nagedachtenis aan het feit dat Gottfried Leibniz aan de Universiteit van Jena bij Erhard Weigel een zomercursus wiskunde volgde. Foto Evergreen68
Na de zomer keert Leibniz terug naar Leipzig en begint daar aan zijn doctoraalstudies rechten en filosofie. In 1666 – hij is dan 20 jaar oud – publiceert hij zijn eerste boek, een filosofieboek getiteld ‘Arte Combinatoria,’ een uitgebreide versie van zijn proefschrift. Het is ten tijde van de publicatie van dit boek dat hij zijn naam verandert van Leibnütz in Leibniz.
Een lectoraat in de rechten aan de universiteit van Leipzig, iets wat hij graag wil, gaat aan zijn neus voorbij. Volgens Leibniz zit de vrouw van de decaan hierachter – helaas vermeldt Leibniz niet waarom zij hier op tegen is; we zijn wel nieuwsgierig naar wat er zich tussen de jonge Leibniz en de vrouw van de decaan heeft afgespeeld. Volgens andere bronnen is de werkelijke reden dat Leibniz geen lectoraat krijgt het feit dat er dat jaar nog twaalf andere kandidaten zijn, die stuk voor stuk eerder aan de beurt zijn om een lectoraat te krijgen – dat gaat op volgorde van afstuderen. Leibniz moet zijn beurt afwachten, zegt de universiteit.
Daar heeft hij geen zin in en als zijn moeder overlijdt en hij geen banden meer met Leipzig heeft, dient hij het al door hem geschreven rechtenproefschrift niet in en vertrekt naar de kleine Universiteit van Altdorf, waar hij in februari 1667 promoveert in de rechten op basis van zijn al in Leipzig geschreven proefschrift, getiteld ‘de Casibus Perplexist’ (‘over Ingewikkelde Zaken’; uiteraard te moeilijk om hier in een paar zinnen uit te leggen).
Leibniz combineert in het proefschrift ideeën over het vak rechten met die uit de filosofie en wiskunde. De universiteit van Altdorf biedt hem vervolgens een professoraat aan, maar Leibniz slaat het aanbod voor de leerstoel af.
In maart 1667 treedt hij als secretaris in dienst van het Alchemistische Genootschap van Neurenberg. Wat het genootschap precies allemaal doet is onduidelijk. De leden hebben een geheimhoudingsplicht – ook Leibniz heeft zich nooit over zijn werkzaamheden uitgelaten – maar vermoedelijk zijn de leden op zoek naar de zogeheten ‘Steen der Wijzen’, een substantie waarvan men gelooft dat met behulp van die materie men gewone metalen in edelmetalen zoals goud kan veranderen. Ook zou het geneeskrachtige werking hebben en het leven kunnen verlengen.
Soms ontdekken alchemisten bij hun experimenten om de Steen der Wijzen te vinden bruikbare nevenproducten. Zo ontdekt de Duitser Hennig Brand in 1669, terwijl hij op zoek is naar de Steen der Wijzen bij het inkoken van menselijke urine fosfor. (Tien jaar later zou Leibniz, als hij in dienst is van de hertog van Hannover, Brand voorzien van grote hoeveelheden urine afkomstig uit de latrines van mijnwerkers die werken in de mijnen van de hertog.)
Leibniz zelf doet geen experimenten, maar zal gedurende zijn hele leven wel in de alchemie geïnteresseerd blijven. Hij zal later regelmatig bevriende alchemisten financieren. Dat kost hem tot zijn teleurstelling meer geld dan dat hem opbrengt. Tegen een vriend klaagt hij in een brief dat het aan de ene kant fijn zou zijn als het maken van goud wat goedkoper kan, maar dat aan de andere kant dit dan wel weer de prijs van goud zal doen dalen.
In november 1667 ontmoet hij baron Johann Christian von Boineburg, de voormalig eerste minister van de keurvorst van Mainz. Von Boineburg neemt hem als assistent in dienst. Als Von Boineburg even later opnieuw in dienst treedt bij de keurvorst (Johann Philipp von Schönborn) volgt Leibniz hem naar Mainz en treedt hij ook in dienst van de keurvorst, in eerste instantie als assistent van de juridisch adviseur.
Aan het hof valt op juridisch gebied het nodige werk te verrichten. Het Duitse recht is in die tijd een wanordelijke combinatie van Romeins recht, ongeschreven traditioneel Duits recht en jurisprudentie uit diverse Duitse vorstendommen. Er is geen overkoepelende Duitse staat met een uniforme wet. Het land bestaat in die tijd uit een groot aantal deelstaten. Na de Dertigjarige Oorlog, waarbij veel Europese landen betrokken zijn en die wordt afgesloten met de vrede van Westfalen in 1648 – de Vrede van Münster uit 1648 tussen Nederland en Spanje maakt hier onderdeel van uit – bestaat de macht van de Duitse Keizer, tevens Keizer van het Heilige Roomse Rijk, eigenlijk alleen nog maar op papier. De feitelijke macht in Duitsland is in handen van de keurvorsten van de vele deelstaten, waaronder die van Mainz.
Leibniz onderneemt pogingen om een uniform rechtstelsel te formuleren maar zal daar uiteindelijk niet in slagen. Een ander project wat hij ook niet succesvol zal voltooien is het samenstellen van een indexboek waarin staat aangegeven in welke bibliotheken in Europa wetenschappelijke boeken staan. Leibniz is erg geïnteresseerd in de wetenschap, niet alleen in de filosofie en het recht, maar ook in die van veel andere terreinen zoals de wiskunde. Hij vindt dat alle wetenschappelijke boeken voor iedereen beschikbaar moeten zijn. Een praktische probleem is echter dat niet bekend is welke boeken bestaan en waar men deze boeken kan vinden.
Leibniz besluit om te onderzoeken of het mogelijk is om indexboeken samen te stellen, waarin je kan opzoeken waar je welke wetenschappelijke boeken kan vinden. Een soort Google avant la lettre. Hij legt daartoe contact met allerlei wetenschappers in Europa maar zal het project niet succesvol afronden. Wel levert het hem contacten op met vele wetenschappers in Europa. Hij begint vaak een uitgebreide briefwisseling met hen. Meestal correspondeert hij in het Frans – zelfs met mede-Duitsers – soms in het Latijn. Uiteindelijk zal hij met meer dan 600 wetenschappers corresponderen. Het totaal aantal geschreven brieven in zijn leven wordt op zo’n 15.000 stuks geschat. Sommigen bestaan uit slechts één A4-tje, anderen zijn hele epistels. Bij elkaar omvatten naar schatting de schrijfsels van Leibniz zo’n 200.000 pagina’s.
Dat Leibniz zo veel brieven schrijft, komt mede doordat er in die tijd nog maar weinig wetenschappelijke tijdschriften bestaan. Geleerden wisselen veelal hun ideeën uit door middel van brieven. Leibniz is sowieso een fanatiek schrijver. Van de site van de VVV-Hannover: ‘De permanent rusteloze geleerde was altijd druk bezig met het op stukjes papier krabbelen van zijn ideeën of het vastleggen van de essentie van gesprekken die hij had gevoerd. Hij gooide al deze biljetten in een grote kast om ze er dan later weer uit te vissen.’
Eén van de schrijfsels van Leibniz. Deze is geschreven in 1716, een half jaar voor zijn overlijden; Afbeelding Bibliotheca Gymnasii Altonani (Hamburg)
Leibniz houdt zich voor de keurvorst ook bezig met diplomatie. Zo publiceert hij in 1669 een vlugschrift over de Poolse troonopvolging – er zijn vier kandidaten voor de troon en de keurvorst heeft een voorkeur voor een kandidaat van Duitse afkomst. Leibniz schrijft het vlugschrift onder het pseudoniem van een fictieve Poolse edelman. Fake news zouden wij nu zeggen. De Duitse kandidaat zal het uiteindelijk niet worden.
Urgenter dan de Poolse troonopvolgingskwestie is voor de Duitse deelstaten de dreiging die Frankrijk vormt. De Franse Zonnekoning Lodewijk XIV heeft in 1667 zijn leger met 30.000 man uitgebreid tot meer dan 80.000 soldaten en dreigt daarmee naar het noorden te trekken. In eerste instantie is zijn doel het gebied van de Spaanse Nederlanden en Holland, maar de Duitse keurvorsten vrezen dat de Fransen daarna richting Duitsland willen gaan.
Leibniz komt op het idee om een poging te wagen de Fransen te verleiden hun blik de andere kant op te richten en wel richting Egypte, waarna ze zouden kunnen doorstoten naar de rijke Indische gebieden van Holland. Hij legt deze gedachte voor aan de keurvorst. De keurvorst zendt Leibniz daarop naar Parijs om contacten met de Franse regering te leggen en hen warm te maken voor dit idee. Erg succesvol is Leibniz hierin niet en in 1672 trekken de Fransen naar het noorden en vallen Holland binnen.
Leibniz, wiens Egypte-plan in duigen is gevallen, blijft in Parijs wonen en verricht daar allerlei diplomatieke werkzaamheden voor de keurvorst. Ook stuurt Von Boineburg, Leibniz zijn andere werkgever, zijn zoon naar hem toe om lessen bij hem te volgen. Tijdens deze periode legt Leibniz contact met diverse in Parijs verblijvende wetenschappers. Eén van hen is de natuur- en wiskundige Christiaan Huygens, die er werkzaam is als onderzoeksdirecteur bij de Franse Academie van Wetenschappen. Huijgens heeft zich in 1666 in Parijs gevestigd. Hij blijft daar ook tijdens de Hollands-Franse oorlog wonen en werken. Hij keert pas in 1681 terug naar Den Haag.
Na gesprekken met Huijgens komt Leibniz tot de conclusie dat hij een grote wiskundige kennisachterstand heeft (hijzelf; niet Huygens) en gaat bij hem in de leer. Het is tijdens deze periode dat Leibniz bedenkt dat je met een rekenmachine veel tijd zou kunnen besparen. “Het is beneden de waardigheid van uitstekende mannen om hun tijd te verspillen met rekenen, terwijl elke boer het werk net zo nauwkeurig zou kunnen doen met behulp van een machine.”, aldus Leibniz in een brief.
In een andere brief schrijft hij: “En nu we de machine een laatste keer mogen prijzen, kunnen we zeggen dat het wenselijk is voor iedereen die zich bezighoudt met berekeningen zoals de beheerders van financiële zaken, de beheerders van andermans landgoederen, kooplieden, landmeters, geografen, navigators, astronomen en degenen die wiskunde gebruiken.”
Leibniz besluit om zelf een dergelijke machine te ontwerpen. Hij heeft een idee gebaseerd op het principe van een hodometer en bedenkt een rekenmachine waarmee je niet alleen kan optellen en aftrekken – dat kan de rekenmachine van Pascal ook; Leibniz is overigens niet op de hoogte van het bestaan van deze rekenmachine – maar waarmee je ook kan vermenigvuldigen en delen.
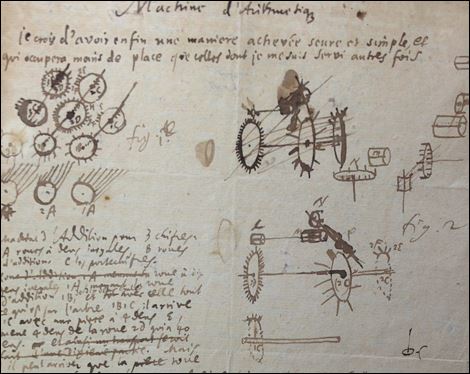
Aantekeningen van Leibniz met daarin wat tekeningen van tandradaren voor zijn machine. En hieronder een voorbeeld met een doorgekraste tekening. Beiden afbeeldingen afkomstig van de site van Stephan Wolfram.
Het geniale aan het ontwerp van Leibniz is zijn idee voor wat later het “Leibnizwiel” is gaan heten. Het is een cilinder met negen ‘tanden’ van verschillende lengtes. Afhankelijk van de waarde van het invoergetal raken deze tanden wel of niet een ander tandwiel dat op zijn beurt weer andere tandwielen in beweging zet.
Links de originele tekening van het wiel zoals Leibniz dat in 1685 schetst in een artikel getiteld ‘Machina arithmetica in qua non additio tantum et sed et mutiplicatio nullo, diviso vero paene nullo animi labore peragantur”. (Die titel had wel wat korter gekund.); rechts een modern voorbeeld van het Leibniz-wiel. Afbeelding: Barbarah
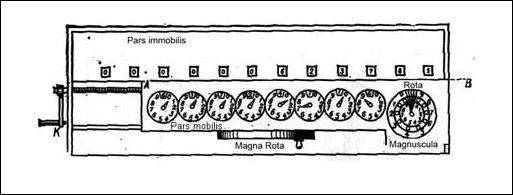 Nog een tekening van Leibniz. Het betreft hier het bovenaanzicht van de machine, waar aan de bovenkant de uitkomst van de berekening verschijnt. Doordat er maar ruimte is voor twaalf vakjes met cijfers, geeft de machine geen uitkomst weer van berekeningen die resulteren in een uitkomst groter dan twaalf cijfers (dat is 1000 miljard; dat is dus niet zo erg.). Rechtsonder (de grote cirkel) bevindt zich de zogenaamde ‘Rota Magnuscale’ waarmee je in stappen het getal invoert waarmee je wilt vermenigvuldigen.
Nog een tekening van Leibniz. Het betreft hier het bovenaanzicht van de machine, waar aan de bovenkant de uitkomst van de berekening verschijnt. Doordat er maar ruimte is voor twaalf vakjes met cijfers, geeft de machine geen uitkomst weer van berekeningen die resulteren in een uitkomst groter dan twaalf cijfers (dat is 1000 miljard; dat is dus niet zo erg.). Rechtsonder (de grote cirkel) bevindt zich de zogenaamde ‘Rota Magnuscale’ waarmee je in stappen het getal invoert waarmee je wilt vermenigvuldigen.
 Een moderne reconstructie van de rekenmachine van Leibniz; afbeelding Eremeev; Wikipedia.
Een moderne reconstructie van de rekenmachine van Leibniz; afbeelding Eremeev; Wikipedia.
Eind 1672 heeft Leibniz een min of meer werkend apparaat, maar het eerste prototype van het ‘Instrumentum Arithmeticum’, zoals Leibniz zijn ‘houten kastje’ noemt, functioneert nog niet helemaal goed. Toch geeft Leibniz in januari 1673 een demonstratie van zijn rekenmachine aan Huijgens en enkele van diens collega’s bij Franse Academie van Wetenschappen. Ook aanwezig is de minister van Financiën Jean-Baptiste Colbert. Huijgens is enthousiast over de mogelijkheden van de machine en als Leibniz vertelt dat hij voor een diplomatieke missie naar Londen moet, schrijft Huijgens een aanbevelingsbrief voor hem, zodat hij zijn rekenmachine ook kan demonstreren aan de wetenschappelijke Royal Society of London.
Op 1 februari 1673 geeft Leibniz daar een presentatie. Hoewel de machine ook bij die gelegenheid niet vlekkeloos functioneert, zijn de leden enthousiast en bieden hem ter plekke het lidmaatschap van de Society aan – op 19 april 1673 wordt hij officieel gekozen tot lid – en vragen ze hem om het apparaat verder te ontwikkelen. (Of Newton ook aanwezig is bij de demonstratie is niet bekend. Het zou kunnen, hij was in 1672 lid geworden.)
Na terugkeer in Parijs krijgt Leibniz te maken met tegenslagen. In december 1672 overlijdt Von Boineburg en twee maanden later ook de keurvorst van Mainz, waardoor Leibniz in korte tijd zijn beide werkgevers verliest. Gelukkig voor hem houdt de weduwe van Von Boineburg hem nog in dienst als studiebegeleider van haar zoon en kan hij in Parijs blijven wonen.
Tijdens deze periode in Parijs ontwikkelt Leibniz zich niet alleen steeds meer als wiskundige – het is in deze jaren dat hij zijn theorie van de differentiaalrekening en de integraalrekening bedenkt – en als filosoof, maar ook houdt hij zich bezig met het bedenken van allerlei apparaten. Zo heeft hij ideeën voor een nieuw type horloge, een apparaat om de positie van een schip op zee te bepalen zonder gebruik te maken van een kompas of de positie van de sterren, een soort onderzeeër en een barometer die niet op kwik werkt maar op uitzetting en krimp van metaal. Bij al deze ideeën loopt hij echter steeds tegen dezelfde problemen als bij zijn rekenmachine aan. De technici zijn niet in staat om zijn ideeën om te zetten in een goed werkend apparaat. Zo wordt zijn idee voor een zogenaamde aneroïde- barometer uit 1698 pas in de negentiende eeuw gerealiseerd en de meeste andere ideeën helemaal niet.
Ook met zijn rekenmachine wil het niet echt vlotten en op 15 maart 1679 – een historische datum, eentje om bij stil te staan – schrijft Leibniz (hij is dan 32 jaar oud) een artikel van drie pagina’s getiteld ‘De Pogressione Dyadica’. In dit artikel over het gebruik van binaire getallen schrijft hij ook over het idee van een rekenmachine die binair werkt (met enen en nullen). Het is een machine zonder wielen of cilinders maar die alleen gebruikt maakt van ballen, gaten, stokken en kanalen voor het transport van de ballen. Hiermee beschrijft hij min of meer het concept van een moderne digitale computer.
Leibniz schrijft: “De volgende methode zou zeker heel gemakkelijk te implementeren zijn. Deze calculus zou kunnen worden geïmplementeerd door een machine zonder wielen maar voorzien […] van gaten zodat deze geopend en gesloten kunnen worden. Ze moeten open zijn op de plaatsen die overeenkomen met een 1 en gesloten blijven op de plaatsen die overeenkomen met een 0. Door de geopende poorten vallen kleine blokjes of knikkers in kanalen, door de anderen niets. […] Geen enkele bal mag van het ene kanaal naar het andere kunnen gaan, behalve wanneer de machine in beweging wordt gebracht. Dan lopen alle knikkers het volgende kanaal in en wanneer er een in een open gat valt, wordt deze verwijderd.”
 Het door Leibniz handgeschreven artikel. (Ik kan het hier wel groter plaatsen maar ook dan zal u het kriebelige handschrift van Leibniz niet kunnen lezen.)
Het door Leibniz handgeschreven artikel. (Ik kan het hier wel groter plaatsen maar ook dan zal u het kriebelige handschrift van Leibniz niet kunnen lezen.)
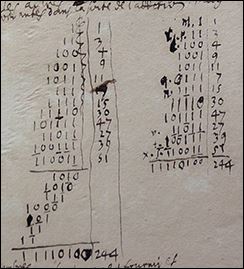
En zie hier twee voorbeelden waarin Leibniz met het binaire stelsel aan het rekenen is. Eentje uit zijn aantekeningen en eentje uit een artikel.
In september 1674 is de zoon van de weduwe Von Boineburg klaar met studeren en stopt zij met betalen. Leibniz zit nu zonder inkomen. Hij wil graag in Parijs blijven wonen maar kan niemand vinden die hem in dienst wil nemen. Ook de Académie van Parijs – zijn gedroomde werkgever – neemt hem niet in dienst. Zelfs het publiceren van een nieuw formule om het getal pi te berekenen helpt hem niet. Zie hier zijn formule:
Als in 1676 zijn schulden steeds verder oplopen, accepteert hij met de nodige tegenzin een baan als bibliothecaris van Johan Friedrich von Braunschweig-Lüneburg, dat is de hertog van Hannover. Het is niet echt zijn droombaan maar het geeft hem wel een vast inkomen.
Voordat hij naar Hannover vertrekt, reist hij echter eerst nog naar Londen – daar bezoekt hij met de nodige schroom (zijn rekenmachine functioneert nog steeds niet goed) de Royal Society – en daarna reist hij af naar Holland.
In Amsterdam gaat hij op bezoek bij Antonie van Leeuwenhoek die hem zijn microscoop demonstreert. In Den Haag bezoekt Leibniz collega-filosoof Spinoza. Ze praten uitgebreid – hij verblijft er vier dagen – over hun filosofische ideeën. Zowel Leibniz als Spinoza gelden als rationalisten die stellen dat de werkelijkheid alleen maar met de rede te doorgronden is. ‘Cogito ergo sum‘ – ‘Ik denk, dus ik ben’ – zoals rationalist René Descartes in 1637 schrijft. (Volgens het rationalisme is de waarneming bedrieglijk. Alleen het zuivere denken levert volgens hen de enige ware kennis van de wereld op. Hier tegenover staat het empirisme dat stelt dat kennis van de wereld alleen maar door waarnemingen verkregen kan worden.)
Na zijn bezoek aan Spinoza reist Leibniz naar Duitsland, waar hij in december 1676 arriveert. Hij zal daar tot aan zijn dood in 1716 voor de hertog van Hannover werken. Aanvankelijk in dienst van Johan Friedrich en na diens overlijden in 1679 in dienst van zijn opvolgers. In Hannover is Leibniz in principe aangenomen als bibliothecaris. Tot zijn taken behoren het beheren van de administratie, het doen van aankopen van boeken en het organiseren van de bibliotheek – tot drie keer toe verhuist de bibliotheek naar een groter gebouw; bij één van die verhuizingen krijgt Leibniz ruzie met de hertog van dienst. Leibniz wil een thematische indeling, de hertog wil dat de boeken op alfabetische volgorde op auteursnaam staan. De wil van de hertog geschiedt.
Het grootste gedeelte van zijn tijd houdt Leibniz zich echter niet met de bibliotheek bezig maar met andere zaken. Vooral met de wetenschap – in 1682 richt hij het wetenschappelijke tijdschrift ‘Acta Eruditorum’ op waarin hijzelf ook veelvuldig publiceert. Ook blijft hij corresponderen met honderden wetenschappers. Ondertussen werkt hij hard aan de voltooiing van zijn differentiaaltheorie. Tevens publiceert hij een werk over verzekeringsstatistiek.
Leibniz treedt ook op als politiek en technisch adviseur van de hertog. Zo is Leibniz tussen 1679 en 1687 druk doende met een probleem dat de hertog heeft met zijn mijnen in het Harzgebergte – deze lopen vaak onder water. Leibniz bedenkt allerlei technische oplossingen om het water uit de mijnen te pompen, maar echt werken doen zijn apparaten (onder andere een nieuw type windmolen en schroefpompen) niet. Hij krijgt er de mijnen niet mee droog. Volgens Leibniz ligt dat aan de arbeiders die zijn ontwerpen opzettelijk verkeerd bouwen, volgens anderen komt het omdat de plannen van Leibniz niet goed zijn uitgewerkt.
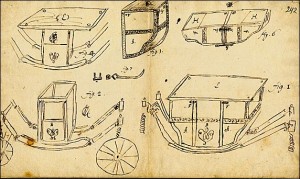
Ook veel andere technische ideeën die Leibniz in de loop van de tijd heeft, bijvoorbeeld voor maliënkolderoverhemden, de vervaardiging van porselein, het gebruik van restwarmte van schoorstenen en een nieuw type – beter verende – koets leiden meestal niet tot een praktisch resultaat. Een uitzondering hierop is zijn idee voor een inklapbare reisstoel. Die komt wel in productie. Helaas voor hem is Leibniz zo’n beetje de enige die daadwerkelijk met zo’n stoel rond reist.
Links Het ontwerp van Leibniz voor een beter verende reiskoets; rechts de stoel van Leibniz; Afbeeldingen LeibnizCentral
In 1687 geeft de hertog van Hannover (dat is op dat moment hertog Ernst Augen) Leibniz de opdracht om de familiegeschiedenis van het geslacht Welfen – hier vormen de hertogen een belangrijke tak van – te onderzoeken. In het kader daarvan reist Leibniz drie jaar lang door Europa, waarbij hij onderzoek doet in allerlei archieven, onder andere in Oostenrijk en Italië. Ter plekke legt hij ook contact met wetenschappers. Tijdens zijn verblijf in Rome wordt hij gekozen als lid van de Academie voor Wis- en Natuurkunde aldaar.
Leibniz werkt hard aan de familiekroniek, maar schiet niet erg op. Voor wat betreft de familiegeschiedenis gaat hij namelijk wel heel erg ver terug in de tijd. Hij onderzoekt onder de paraplu van research voor de familiekroniek zelfs hoe mineralen zijn ontstaan, bestudeert de grote volksverhuizingen in Europa uit de oudheid en onderzoekt hoe verschillende talen tot stand zijn gekomen. Dat allemaal onder het mom van stamboomonderzoek. Nog een mooi voorbeeld: in Rome onderzoekt hij het gerucht dat er ooit een vrouwelijk paus is geweest (volgens Leibniz was dat niet het geval maar hij publiceert niet de resultaten van zijn onderzoek. )
Een blad met aantekeningen van Leibniz voor het familieonderzoek. Deze gaat over een gebeurtenis in 1212; Bron LeibnizCentral
Over de voortgang van zijn onderzoek naar de geschiedenis van het huis Welfen schrijft Leibniz in 1695 in een brief aan een zekere Vincent Placcius: “Ik kan niet eindigen met je te vertellen hoe buitengewoon afgeleid en verstrooid ik ben. Ik probeer verschillende dingen in deze bestanden te vinden; Ik zoek oude papieren en ga achter ongepubliceerde documenten aan. Hiermee hoop ik enig licht te werpen op de geschiedenis van het Huis. Ik ontvang en reageer op een enorm aantal brieven. Tegelijkertijd heb ik zoveel wiskundige resultaten, filosofische gedachten en andere literaire vernieuwingen, die niet mogen vervagen, dat ik vaak niet weet waar ik moet beginnen.” Kortom, Leibniz is net als uw schrijver snel afgeleid.
Omstreeks 1700 publiceert hij eindelijk de eerste zes delen van de geschiedenis van de familie Welfen. Tien jaar later nog eens drie grote delen en als hij op 14 november 1716 naar een kortstondig ziekbed overlijdt, is hij nog steeds niet klaar met de familiegeschiedenis.
Dat komt mede omdat hij ook veel tijd heeft verloren met zijn pogingen om academische genootschappen op te richten in Berlijn, Dresden, Wenen en in Sint-Petersburg – in het kader van die in Sint Petersburg spreekt hij een aantal keer met Tsaar Peter de Grote. Ook bemoeit hij zich met veel erfopvolgingskwesties bij koningshuizen in Europa. Hij geldt als autoriteit op dat gebied. Ook in China is hij erg geïnteresseerd. Daartoe correspondeert hij met meerdere jezuïeten die als missionarissen in China werkzaam zijn geweest. Over China – hij is er overigens nooit geweest – schrijft hij in 1697 het boek ‘Novissima Sinica’.
Hij schrijft ook veel over filosofische zaken. Zo publiceert Leibniz in 1710 zijn filosofische verhandeling ‘Théodicée’. Het is dit boek waarin hij schrijft dat, ook al zit de wereld vol met allerlei ellende, het toch de best mogelijke wereld is die God heeft kunnen schapen.
Links Leibniz’ boek over China uit 1697; Rechts. Leibniz’ Theodicee uit 1710
Om een lang verhaal kort te maken – wat niet meer kan want dit verhaal is al lang – tot aan zijn dood in 1716 blijft hij een druk baasje. Zo stelt hij in 1715 de Engelsen nog voor om hem tot de officiële geschiedschrijver van Engeland te benoemen. Ze gaan niet op het aanbod in. Ook werkt hij aan verbeteringen voor zijn rekenmachine. Tot een volledig goed werkend exemplaar komt het echter nooit. Wel is het zo dat tot tweehonderd jaar na zijn overlijden in elke analoge rekenmachine een Leibniz-wiel zit.
 Het enige nog originele bestaande exemplaar van de (vermoedelijk minstens tien) exemplaren die Leibniz tijdens zijn leven liet bouwen. Het bevindt zich thans in de Niedersächsische Landesbibliothek (GWLB) in Hannover; foto Gottfried Wilhelm Leibniz Bibliothek – Niedersächsische Landesbibliothek.
Het enige nog originele bestaande exemplaar van de (vermoedelijk minstens tien) exemplaren die Leibniz tijdens zijn leven liet bouwen. Het bevindt zich thans in de Niedersächsische Landesbibliothek (GWLB) in Hannover; foto Gottfried Wilhelm Leibniz Bibliothek – Niedersächsische Landesbibliothek.
Leibniz blijft zijn hele leven vrijgezel. Er zijn geen relaties van hem met mannen of vrouwen bekend. Waarschijnlijk heeft hij het er gewoon te druk voor. Over zijn persoonlijke leven is dan ook weinig bekend. Alleen de VVV van Hannover weet op hun site hier iets over te melden: ‘Leibniz was een imposante figuur, vooral in Hannover. Normaal droeg hij een lange zwarte pruik, zoals gebruikelijk was aan het hof. Hij hechtte veel belang aan persoonlijke hygiëne. Hij bezocht kuuroorden om van het water te genieten en had duidelijk een aangename lichaamsgeur. Dit was destijds zeer zeldzaam en blijkt uit brieven die vrouwelijke bewonderaars hem hebben gestuurd. Hij droeg geborduurde jassen, een das, knielange kousen met lange kousen en schoenen met gespen. Hij had zijn koets met fluweel bekleed en gebruikte hem vaak om naar zijn tuin te reizen, in de buurt van wat nu Aegidientorplatz is, waar hij tabak plantte en moerbeibomen verbouwde om zijderupsen te kweken.’
Daar moeten we het voor wat betreft zijn persoonlijke leven mee doen. Na een werkzaam leven, zoals dat zo mooi heet, sterft Leibniz op 14 november 1716 na een kort ziekbed op 70-jarige leeftijd in Hannover.
Tot slot, de meeste Duitsers kennen Leibniz vandaag de dag niet als wiskundige of filosoof maar alleen als koekje.
Een Leibniz Butterkeks; foto Rainer Zenz
Het boterkoekje wordt in 1891 door het bedrijf Bahlsen voor het eerst op de markt gebracht om te concurreren met het Franse ‘Petit-Beurre’ koekje. Het is in die tijd mode om voedselproducten te vernoemen naar historische beroemdheden. Bahlsen, gevestigd in Hannover, kiest voor Leibniz, de bekendste inwoner uit de geschiedenis van de stad.
Er bestaat overigens ook een Newton koekje (een koekje met jam, bedacht in Amerika.)
Het Newton koekje
En weet u in welk jaar het Newton koekje voor het eerst op de markt verscheen? Inderdaad, net zoals het Leibniz koekje, in 1891. Het is niet bekend welk koekje exact als eerste op de markt verscheen. Ongetwijfeld zullen de meningen er over verdeeld zijn.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie