Heeft u zich op school wel eens het hoofd moeten breken over het probleem van twee auto’s die zich op een afstand X van elkaar bevinden en die met bepaalde snelheden naar elkaar toe rijden, waarbij de vraag is waar en wanneer ze elkaar tegen komen? Troost u dan met de gedachte dat studenten in de dertiende eeuw zich ook al met dit probleem hebben moeten bezig houden, alleen toen betrof het uiteraard geen auto’s die naar elkaar toe reden, maar twee slangen die naar elkaar toe kropen. De vraag was waar komen die twee slangen elkaar tegen?
Het was een opgave uit het boek ‘Liber abaci’ van Leonardo da Pisa. Met dit boek liet hij in Europa het grote publiek voor het eerst kennis maken met de Arabisch-Indische cijfersystematiek inclusief het cijfer 0.
Twee pagina’s van het boek uit 1228 afkomstig uit de bibliotheek van Sienna. Waarschijnlijk heeft degene die het boek in deze staat terug bracht daar wel enige vragen over gekregen.
Leonardo da Pisa – de Latijnse versie van zijn naam luidt Leonardo Pisano – kennen we vandaag de dag vooral onder de naam Fibonacci. Die naam is een samentrekking van de woorden ‘Filius’ en ‘Bonacci’, oftewel ‘Kind’ van ‘Bonacci’. Dit doet vermoeden dat Bonacci de achternaam van zijn vader is, maar dat klopt niet. ‘Bonacci’ was namelijk de bijnaam van zijn grootvader (het betekent zoiets als ’goeierd’). Andere namen waaronder we Leonardo di Pisa kennen, zijn ‘Leonardus Pisanus’, ‘Leonardus filius Bonacij’, ‘Leonardus Pisanus de filiis Bonaccij’, ‘Leonardi Bigholli de Pisa ‘(zo noemt hij zichzelf in een boek uit 1202) en ‘Leonardus Bigollus’ (‘Leonardo die veel heeft gereisd’). Een heel gezelschap, kiest u maar een naam uit.
Omdat we Leonardo da Pisa vandaag de dag vooral kennen onder de naam Fibonacci, zullen we in de rest van dit verhaal deze naam hanteren, al is het wel ironisch dat niemand in zijn tijd hem zo noemde. De naam Fibonacci duikt namelijk pas voor het eerst in de negentiende eeuw op. Het is ene Guillaume Libri die in 1838 in een boek over Fibonacci met deze naam op de proppen komt. Hij baseert zich hierbij op de inleiding van het boek ‘Liber abaci’ dat Leonardo da Pisa in 1202 publiceert. (‘Abaci wordt ook wel eens als ‘abbaci’geschreven.) De inleiding van dit boek begint (vrij vertaald) als volgt: “Dit is het begin van het rekenboek samengesteld door Leonardi zoon van de ‘fibon Bonacci’ opgesteld in het jaar MCCII.”
 De intro van het boek met in de blauwe cirkel de woorden ‘fibon Bonacci’ en in de groene cirkel het getal 1202 (MCCII), hier weergegeven in de Romeinse cijfers.
De intro van het boek met in de blauwe cirkel de woorden ‘fibon Bonacci’ en in de groene cirkel het getal 1202 (MCCII), hier weergegeven in de Romeinse cijfers.
(Tussen haakjes, omdat Leonardo de lezers van het boek in de inleiding de nieuwe schrijfwijze van getallen nog niet heeft uitgelegd, schrijft hij hier het jaartal 1202 nog met hulp van de Romeinse cijfers en niet met de Arabische cijfers 0 t/m 9)
Vermoedelijk heeft Leonardo met de woorden ‘fibon bonacci’ willen aangeven dat hij behoort tot de familie van zijn grootvader Bonacci’. Guillaume Libri trekt echter (ten onrechte) de woorden fibon en Bonacci samen tot Fibonacci en denkt dat dit zijn naam is. Sindsdien kennen we Leonardo da Pisa onder de naam Fibonacci. Herman van Veen zou zeggen: “Alles wat ik heb, is een naam en die heb ik van een ander.”
Wie is Fibonacci?
Hoe hij er uit zag weten we niet. De afbeelding van Leonardo da Pisa die je vaakst ziet, is er eentje die voor het eerst verschijnt in een boek uit 1850. Toen was hij echter al zes eeuwen dood. Gaat u dus maar van uit dat die tekening niet klopt. Datzelfde zal ook gelden voor een bekend standbeeld van Fibonacci uit 1863 gemaakt door de bekende Italiaanse beeldhouwer Giovanni Paganucci.
Waar Fibonacci geboren is, weten we wel, namelijk in Pisa, maar in welk jaar weer niet. Meestal wordt 1170 als zijn geboortejaar vermeld, maar ook 1175 komt wel eens voorbij. Niet dat het er toe doet. Pisa is in die tijd, samen met Venetië en Genua, één van de belangrijkste maritieme republieken die Italië in de Late Middeleeuwen kent. In totaal telt Italië op dat moment acht van dergelijke stadsrepublieken. Het zijn min of meer onafhankelijke staten. Zo hebben ze bijvoorbeeld elk een eigen vloot en leger.
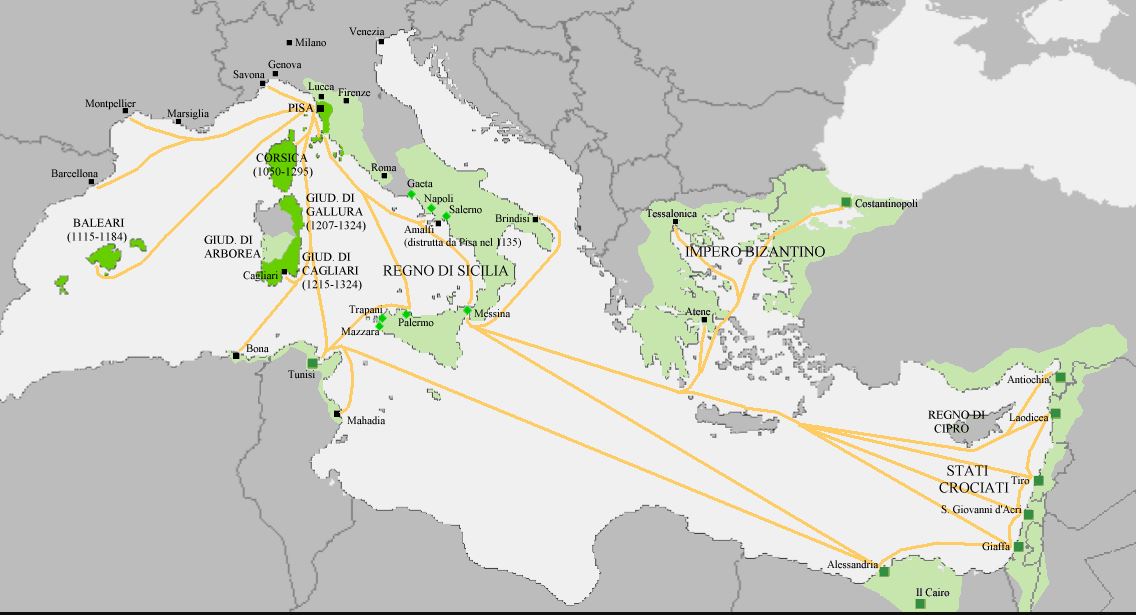
De stadsstaat Pisa bestaat van de 11e tot aan de 15e eeuw. Op onderstaand kaartje is te zien hoe groot de invloed van Pisa op zijn hoogtepunt was. De donkergroene delen op de kaart (Corsica, de Balearen en een groot deel van Sardinië) zijn door Pisa bezette gebieden. Met de lichtgroene gebieden onderhoudt Pisa stevige handelsbetrekkingen en heeft er handelsvestigingen gevestigd. De donkere groene en zwarte blokjes op de afbeelding geven deze vestigingen aan. De gele lijnen laten de belangrijkste handelsroutes van Pisa zien.
In de steden met een handelsvestiging heeft Pisa vertegenwoordigers gestationeerd. Eén van deze mensen is Fibonacci‘s vader Gugliemlo. Hij vertegenwoordigt Pisa in de havenstad Bugia – het huidige Bejaia, een stad in Algerije. (Op het bovenstaande kaartje is Bugia het meest linkse zwarte blokje in Afrika). In de inleiding van zijn boek ‘Liber abaci’ uit 1202 schrijft Fibonacci dat zijn vader ‘een publieke schrijver in douanerechten voor Pisaanse handelaren was in Bugia’.
Fibonacci vermeldt in het boek ook dat hij in Bugia tijdens zijn kindertijd is onderwezen in de Indiaanse getallen – zo noemt hij het Arabisch–Indische getallenstelsel (met de cijfers 1 t/m 9 plus het cijfer ’0’). Hij is erg enthousiast over de mogelijkheden die dit getallenstelsel biedt. “De introductie en kennis van deze rekenkunst beviel me boven alles” zo schrijft hij. Fibonacci komt tot de conclusie dat het met dit getallenstelsel veel gemakkelijker rekenen is dan met het klassieke Romeinse getallenstelsel.
In de jaren daarop verdiept hij zich uitgebreid in het getallenstelsel. Ook bestudeert hij talloze werken van islamitische geleerden, zoals die van al-Khwārizmī. Als hij ouder is, reist Fibonacci, soms in gezelschap van zijn vader, naar verschillende steden in het Middellandse Zeegebied tot aan Constantinopel toe. Het levert hem de bijnaam Leonardus Bigollus op (‘Leonardo die veel heeft gereisd’; had ik deze naam al vermeld?).
Liber abaci’
Omstreeks 1200 keert Fibonacci, hij is dan een jaar of dertig, terug naar Pisa en begint hij te werken aan een wiskundig leerboek dat hij de titel ‘Liber abaci’ zal geven (‘het boek om te rekenen’). Fibonacci beschikte mede dankzij zijn reizen over veel Latijnse, Griekse en Arabische bronnen, die hij gebruikt om zijn boek te schrijven. Het verschijnt in 1202. Het is niet alleen bedoeld als leerboek om zijn lezers te onderwijzen in de kunst van het rekenen met de “nieuwe Indische getallen”, maar ook omvat het hoofdstukken met (wiskundige) oplossingen voor allerlei praktische handelsproblemen.
De eerste pagina – het is een soort inhoudsopgave – van een herziende versie van het boek uit 1228. De rode hoofdletters zijn de beginletters van de hoofdstuktitels van het boek. Helemaal onderop zie je in het rood de ‘nieuwe’ getallen 9 8 7 6 5 4 3 2 en 1 staan. Zie hieronder deze cijfers in detail staan.
Afbeelding afkomstig uit een exemplaar uit 1300 dat zich thans in de Biblioteca Communale di Siena bevindt.
Het boek telt vijftien hoofdstukken. In het eerste hoofdstuk legt Fibonacci het nieuwe Indische’ getallenstelsel, inclusief het cijfer 0 ,uit. “Novem figure indorum he sunt 9 8 7 6 5 4 3 2 1 Cum his itaque novem figuris, et cum hoc signo 0, quod arabice zephirum appellatur.” zo begint hij (in het Latijn) het hoofdstuk. In de volgende vier hoofdstukken laat hij vervolgens zien hoe je met deze getallen kan rekenen.
 Een pagina uit de Liber Abaci. Rechts staan voorbeelden van berekeningen met de ‘Arabische getallen’. Afbeelding: Openbare Bibliotheek Siena
Een pagina uit de Liber Abaci. Rechts staan voorbeelden van berekeningen met de ‘Arabische getallen’. Afbeelding: Openbare Bibliotheek Siena
Ook laat hij zien hoe je met breuken kan rekenen. In de tijd van Fibonacci kent men nog niet het systeem van decimale cijfers achter de komma om fracties van getallen aan te geven. – als bedenker daarvan geldt Al-Kashi (1380 – 1429) – maar schrijft men deze fracties in de vorm van breuken. Fibonacci schrijft in zijn boek het breukgedeelte overigens consequent voor het niet-breukgedeelte van het getal in plaats van er achter wat meer gebruikelijk is.
8,1 = 8 1/10 oftewel 1/10 8 in de schrijfwijze van Fibonacci.
Na de hoofdstukken met de rekenregels vervolgt het boek met vier hoofdstukken die specifiek zijn bestemd voor handelaren. Deze hoofdstukken gaan onder andere over de aan- en verkoop van goederen, ruilhandel, omwisseling van valuta’s en – heel belangrijk voor handelaren – de optimalisering van winst, als je moet kiezen welke producten je moet verhandelen.
Dan volgt er een groot hoofdstuk om te oefenen met de nieuwe getallen. Dit hoofdstuk omvat een derde van het boek. Het bevat allerlei wiskundige opgaves, waaronder als bekendste het konijnenprobleem. ‘Bepaal hoeveel konijnenparen je aan het einde van het jaar hebt, beginnend met één paar, als elk paar vanaf de tweede maand vruchtbaar zal zijn en dan één nieuw paar per maand voortbrengt’. Het oplossen van deze vraag leidt tot de beroemde reeks van Fibonacci. Daar kom ik straks op terug.
Twee andere opgaven uit het hoofdstuk die later zeer bekend zijn geworden, zijn het spinnenprobleem en het reeds eerder vermelde slangenprobleem. Het spinnenprobleem luidt: ‘Een spin klimt overdag een vaste afstand van 30 cm omhoog langs een muur van 2,40 m hoogte, maar glijdt ‘s nachts weer 20 cm terug. Hoe lang duurt het voordat de spin bovenaan de muur is?’ U mag het zelf uitrekenen. (Denkt u dat het 24 dagen duurt, dit omdat de spin netto elke dag 10 cm klimt? Dan heeft u het fout, want op de 22e dag bereikt de spin al de bovenkant van de muur. Oké, hij glijdt daarna die dag weer 20 cm terug, maar hij is boven geweest!) Het zijn typische opgaven voor een leerboek. Het boek wordt afgesloten met drie hoofdstukken met daarin enkele wiskundige beschouwingen.
Van de eerste uitgave van het boek uit 1202 bestaan geen exemplaren meer. In 1228 verschijnt een tweede herziende uitgave. Hiervan hebben een drietal exemplaren de vergankelijkheid van de tijd grotendeels overleeft. Daarnaast bestaan er ook nog elf exemplaren van deze uitgave waarbij kleine of grote delen ontbreken. Van de drie bijna volledige exemplaren bevindt zich er eentje in de bibliotheek van het Vaticaan in Rome, eentje in de bibliotheek van Sienna en eentje in de bibliotheek van Florence.
Met de ‘Liber abaci’ begint de opmars van de Arabisch–Indische cijfers in Europa en verdwijnt langzaam maar zeker het gebruik van de Romeinse cijfers. Nu is Fibonacci niet de eerste die een poging waagt om de Arabisch–Indische (Hindu) cijfers in Europa te introduceren. Zo’n twee eeuwen voor hem is Gerbert van Aurillac (de latere Paus Sylvester II) hem al voor gegaan, al kent deze nog niet het cijfer nul. De poging van Gerbert van Aurillac is verdienstelijk maar niet erg succesvol. Waarschijnlijk komt dat mede omdat hij zich vooral richtte op de wetenschappers onder de geestelijken. Het boek van Fibonacci daarentegen is vooral op de handel gericht en tja, als men ergens geld mee kan verdienen, dan staat men eerder open voor iets nieuws.
Aanvankelijk is er nog wel de nodige weerstand tegen de nieuwe schrijfwijze van de getallen – het stadsbestuur van Florence is bijvoorbeeld lang tegen het gebruik van de nieuwe cijfers. Ze zijn bij voorbeeld bang dat een kwaadwillige de 0 in een schuldbewijs zomaar in een 9 zou kunnen veranderen. Ook de kerk vindt het aanvankelijk maar niks, maar na verloop van tijd wordt door steeds meer mensen gebruik gemaakt van het nieuwe getallenstelsel, eerst in Italië, daarna elders in Europa.
Fibonacci wordt dankzij zijn boek een beroemdheid. Zo wordt hij uitgenodigd door Frederick II – die sinds 1198 niet alleen koning van Sicilië en vanaf 1215 ook de Duitse koning is, maar die daarnaast ook vanaf 1220 dertig jaar lang de keizer van het Heilige Roomse Rijk is. Fibonacci krijgt niet alleen eerbewijzen. Zo ontvangt hij vanaf 1240 van de stad Pisa een jaarlijkse vaste financiële vergoeding vanwege “zijn verdiensten als belastingconsulent en controleur van de stad en voor toekomstige diensten van dit soort”.
Naast zijn ‘Liber abaci’ schrijft Fibonacci nog een aantal andere boeken. In 1220 publiceert hij ‘Practica Geometriae’. In dit boek behandelt hij een groot aantal meetkundige problemen en gaat hij in op het werk van Euclides. Andere door hem geschreven boeken zijn ‘Flos’ (1225) – dit gaat niet over het schoonmaken van het gebit, maar bevat een aantal wiskundige problemen die zijn aangedragen door de wiskundige Johannes van Palermo – en ‘Liber Quadratorum’, eveneens uitgegeven in 1225.
Dit laatste boek is wiskundig gezien Fibonacci’s indrukwekkendste boek. Hij schrijft hierin vooral over kwadraten. Zo onderzoekt hij methoden om getallen te vinden die voldoen aan de formule a2 + b2 = c2 (een voorbeeldje is 32 + 42 = 52). Ook laat hij zien dat als je het kwadraat van n kent, je op een eenvoudige wijze het kwadraat van (n+1) kan vinden. Hij maakt hierbij handig gebruikt van de formule (n + 1)2 = n2 + 2n + 1. Een voorbeeldje: stel n=25 en je weet dat het kwadraat van 25 gelijk is aan 625, dan is het kwadraat van 26 = 25+1 gelijk aan 625 + 2×25 + 1 = 676.
Fibonacci overlijdt ergens tussen 1240 en 1250 – vaak wordt 1242 als het jaar van zijn overlijden genoemd. Hij is waarschijnlijk een jaar of zeventig oud geworden. Nog eeuwenlang zal Fibonacci’s boek overal in Europa als leerboek worden gebruikt, waardoor de Arabisch-Indische cijfernotatie uiteindelijk het getallenstelsel van de wereld wordt.
De reeks van Fibonacci.
Tot slot wil ik nog even terugkomen op het konijnenprobleem. ‘Bepaal hoeveel konijnenparen je aan het einde van het jaar hebt, beginnend met één paar, als elk paar vanaf de tweede maand vruchtbaar zal zijn en dan één nieuw paar per maand voortbrengt’. Het is niet echt iets waar je veel aan hebt, tenzij je wilt bepalen hoe groot je konijnenhok moet zijn. De uitkomst is dat je na twaalf maanden 233 konijnenparen hebt, waarvan er 144 op dat moment vruchtbaar zijn en 89 nog niet vruchtbaar zijn. Het is maar dat u het weet.
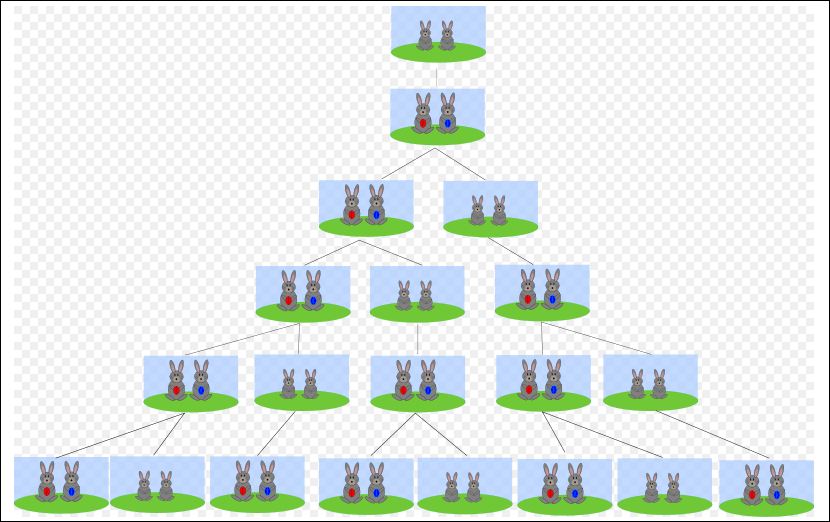
Niet bijster interessant, ware het niet dat Fibonacci bij de tussenberekeningen (van het aantal konijnenparen) laat zien dat het aantal konijnenparen na elke maand gelijk is aan de som van de aantallen van de vorige twee maanden: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233. Zie hieronder een afbeelding uit de Finse versie van de Wikipedia die dit voor de eerste zes maanden grafisch weergeeft.
Visuele weergave van het aantal konijnenparen per maand voor de eerst zes maanden; de konijnenparen met een gekleurd balletje (rood of blauw) zijn vruchtbaar en kunnen elke maand twee jongen krijgen. De jongen zijn de eerste maand nog niet vruchtbaar en hebben in die maand geen gekleurd balletje, een maand later wel.
In zijn boek van Fibonacci ziet de probleembeschrijving en zijn oplossing er als volgt uit.
Ik moet zeggen dat het in de Finse Wikipedia wat duidelijker wordt uitgelegd.
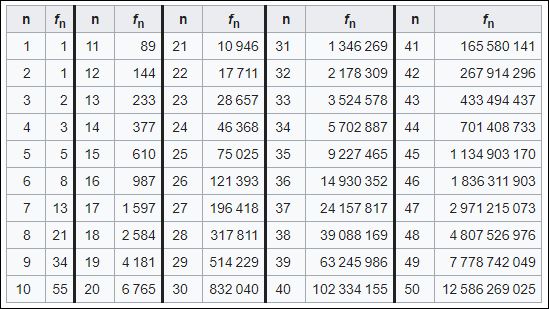
De reeks van Fibonacci gaat eindeloos door. Al snel worden de getallen erg groot. Zo is het 48e getal uit de reeks al bijna 5 miljard. (Na vier jaar heb je met deze voortplantingssnelheid van de konijnen dan ook een gigantisch groot hok nodig.) De eerste vijftig getallen van reeks van Fibonacci luiden:
Fibonacci is niet de eerste die met deze reeks op de proppen komt. Niet alleen de Indiaanse taalkundige Pingala (zie deel 1) kwam al met dezelfde getallenrij op de proppen, maar ook de Indische wetenschapper Virahanka vermeldt de reeks (in de zesde eeuw na Christus) in één van zijn werken. Echter zowel Pingala als Virahanka raken in de vergetelheid, waardoor deze rij van getallen nu bekend staat als de reeks van Fibonacci. De reeks van Fibonacci is echter niet de reden dat hij een plekje heeft gekregen in deze serie over mensen achter de computer. Dat is omdat hij degene is geweest die er voor heeft gezorgd dat het Arabisch-Indische getallenstelsel, inclusief het cijfer nul, in Europa op grote schaal bekend wordt.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie