Links, een Iraanse postzegel uit 1979 met daarop het portret van Al- Kāshī; rechts een afbeelding van Simon Stevin. Ze lijken wel een beetje op elkaar.
De uitdrukking ‘Dit heeft alleen effect achter de komma’ betekent dat iets maar een klein effect heeft. Nu is de Perzische wetenschapper al-Kāshī vooral bekend vanwege zijn ideeën voor ‘achter de komma’, maar dat wil niet zeggen dat zijn ideeën niet van groot belang zijn geweest voor de wetenschap. Al-Kāshī is namelijk degene die het vaakst wordt aangeduid als de bedenker van het idee om door middel van (decimale) cijfers achter de komma een breuk weer te geven. Tot dan toe gebruikte men meestal een a/b notatie om een getal kleiner dan 1 aan te geven. Zo schrijft men 1/8 in plaats van de decimale weergave 0,125. Eén van de redenen om een a/b notatie te gebruiken in plaats van een decimale weergave is dat niet alle breuken 100% exact decimaal kunnen worden weergegeven. Zo is 1/3 gelijk aan 0,3333333… waarbij die drieën maar eindeloos door blijven gaan.
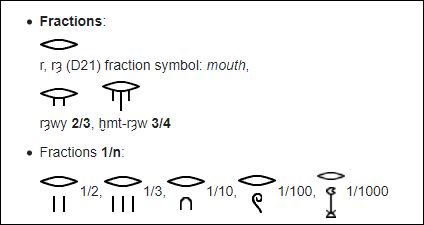
Ook de oude Egyptenaren hadden al symbolen voor breuken.
Naast al Kāshī zijn er nog een aantal mensen die ook in verband met het bedenken van het systeem van decimale breuken worden genoemd zoals Abu’l-Hasan al-Uqlidisi. Deze Arabische wiskundige uit Damascus (± 920 tot ±980) schrijft in 952 een boekwerk getiteld ‘al-Fusu’l’ over het gebruik van de Hindoe-Arabische cijfers. Hij schrijft hierin iets wat kan worden betiteld als het rekenen met decimale cijfers. Of hij echter daadwerkelijk daarmee het rekenen met cijfers achter de komma bedoelde, is echter afhankelijk van de manier waarop men een bepaalde tekst uit het boek interpreteert.
Ook de Fransman Immanuel Bonfils wordt wel eens in verband met de decimale breukennotatie genoemd. Hij zou omstreeks 1350 ook over een dergelijk systeem hebben geschreven. Daarnaast hebben in het verre verleden een aantal Arabische en Chinese wetenschappers zich ook bezig gehouden met decimale breuken, maar dat is nog voor de ‘ontdekking’ van het getal nul en sluit daarom niet goed aan op het huidige systeem van cijfers achter de komma waarin ook de nul in voor kan komen. Meestal wordt daarom al- Kāshī gezien als de ‘bedenker’ van het rekensysteem van decimale breuken.
Echt doordringen tot de rest van de wereld doet zijn werk echter niet. Daarom moeten we het in dit verband ook hebben over de Vlaams-Nederlandse wiskundige Simon Stevin (1548 – 1620). Hij is degene die naast al-Kāshī en al-Uqlidisi het vaakst wordt genoemd in verband met het gebruik van decimale breuken. Simon Stevin is de eerste wetenschapper die een heel boekwerk, getiteld ‘De Thiende’, publiceert over het gebruik van cijfers achter de komma. Hij doet dit in 1585. Dankzij zijn boek maken de decimale breuken een opmars door Europa en de rest van de wereld. Geldt al-Kāshī als de bedenker van het rekenen met decimale breuken, Simon Stevin is degene die wereldwijd wordt gezien als de grote promotor van het idee.
Zou er omstreeks 1600 een Nobelprijs voor wiskunde zijn uitgekeerd voor het idee van de decimale cijfers om breuken aan te geven, dan zou hij gezamenlijk zijn toegekend aan al-Kāshī en Simon Stevin. Klein detail, er bestaat geen Nobelprijs voor wiskunde. (Er bestaan allerlei theorieën waarom Nobel geen Nobelprijs voor de wiskunde in het leven heeft geroepen. Zo zou Alfred Nobel een hekel aan wiskundigen hebben gehad, omdat zijn vrouw ooit vreemd ging met een wiskundige. Een hinderlijk detail bij deze mooie theorie is dat Nobel nooit getrouwd is geweest.)
Maar goed, we hebben dus twee mensen die in verband met decimale cijfers in aanmerking komen voor een plekje in de reeks mensen achter de computer. Als eerste Al- Kāshī:
21a Jamshid Al- Kāshī, ca 1380 – 1429; wiskundige en astronoom, geldt als de bedenker van het systeem van decimale breuken.
Jamshid al-Kāshī komt omstreeks 1380 ter wereld in Kashan, een stad gelegen in een woestijn zo’n 200 km ten zuiden van Teheran. Zijn volledige naam luidt: Ġiyāṯ ad-Dīn Ǧamšīd bin Masʿūd bin Muḥammad al Tabib al-Kāšī. We kennen hem kortweg als al-Kāshī.
Analyseren we zijn naam, dan komen we al heel wat te weten over hem. ‘Ġiyāṯ ad-Dīn’ betekent ‘behoeftige dienaar van God’ – hij was dus een godsdienstig iemand; ‘Ǧamšīd’ is zijn voornaam; ‘Masʿūd’ de naam van zijn vader; ‘Muḥammad’ de naam van zijn grootvader; ‘al Tabib’ betekent dokter; en tot slot: ‘al-Kāshī’ (de naam waaronder wij hem kennen) houdt in dat hij uit de plaats Kashan kwam. Onduidelijk is wie de dokter in de familie is. Het kan zowel al-Kāshī zelf zijn, maar ook zijn vader of zijn grootvader. Vermoedelijk is het zijn vader die de dokter is. Kashan, de geboorteplaats van Al-Kāshī, maakt eind veertiende eeuw deel uit van het Timoeridische rijk, een rijk gesticht door Timoer Lenk (ook wel bekend als Timoer de Manke – hij had een oude oorlogswond.) Het omvatte zo’n beetje het huidige Iran en Turkmenistan.
Timoer Lenk is een oorlogszuchtig persoontje die zijn hele leven bezig is om met veel geweld zijn rijk te vergroten. Het is dan ook geen tijd waarin de wetenschap kan floreren. In 1405 sterft Timoer en wordt hij opgevolgd door zijn zoon Shah Rukh. In tegenstelling tot zijn vader is Shah Rukh, en vooral diens vrouw Gawhar Shad, een Turkse prinses, wel geïnteresseerd in de wereld van de kunst en wetenschap. Dat verbetert het leven van wetenschappers zoals al-Kāshī dan ook aanmerkelijk.
Van de eerste vijfentwintig jaar van het leven van al-Kāshī – de tijd dat Timoer de Manke regeert – weten we weinig. Volgens sommige bronnen zou al-Kāshī in bittere armoede zijn opgegroeid en op verschillende plaatsen in (het huidige) Iran hebben gewoond, maar of dat klopt is niet zeker. Vanaf het jaar 1405 weten we meer over hem, vooral dankzij zijn eigen boeken, die hij zeer nauwkeurig dateert en waarin hij vaak over zijn wonen en werken schrijft. Ook zijn er een tweetal brieven van hem aan zijn vader uit 1424 bewaard gebleven. Deze brieven suggereren dat zijn vader niet alleen arts is maar ook een erudiet man, wat doet vermoeden dat al-Kāshī veel van zijn wetenschappelijke basiskennis bij zijn vader heeft opgedaan.
In juni 1406 duikt al-Kāshī voor het eerst op in de geschiedenisboeken. In een geschrift maakt hij melding van een maansverduistering die hij op 2 juni heeft waargenomen in Kashan. In 1407 verschijnt er van zijn hand een astronomisch werk getiteld ‘Sullam al-samāʾ, wat zoiets betekent als ‘de ladder naar de hemel’. (Vijf eeuwen later zou de popgroep Led Zeppelin een popsong met een soortgelijke titel (Stairway to Heaven) uitbrengen, maar dat staat hier uiteraard geheel los van.)
In 1410 verschijnt er wederom een astronomieboek van zijn hand, dat hij opdraagt aan ene Kamāl al‐Dīn Maḥmūd, een grootvizier. Wetenschappers zoeken in die tijd vaak een beschermheer, dit in de hoop dat deze hen van een inkomen zal voorzien. Achteraf bekeken is de keuze voor deze plaatselijke grootvizier niet zo’n gelukkige, want de grootvizier wordt even later geëxecuteerd door iemand waarmee hij ruzie heeft en die hoger in rang is.
Een volgend astronomisch boek uit 1411 draagt al-Kāshī op aan Sultan Iskandar, een neef van Shah Rukh. Blijkbaar is ook hij niet de juiste beschermheer, want zijn volgende boek, ‘Khāqānī Zīj’ – een boek uit 1413 met allerlei astronomische tabellen; het bevat ook een tabel met de coördinaten van 515 plaatsen op Aarde – draagt al-Kāshī op aan Ulūgh Beg, de zoon van Shah Rukh, de hoogste machthebber in het land. Deze Ulūgh Beg is zelf ook wetenschapper en heeft veel waardering voor het werk van al-Kāshī. Onduidelijk is echter of hij al-Kāshī al in 1413 financieel gaat ondersteunen, vermoedelijk nog niet.
Een pagina uit ‘Khāqānī Zīj’, het boek van al-Kāshī uit 1413. Het exemplaar bevindt zich in de Astan Quds Razavi bibliotheek in Mashad, de op een na grootste stad van het huidige Iran.
In 1416 brengt de erg actieve al-Kāshī zelfs twee astronomieboeken uit die hij beide opdraagt aan Ulūgh Beg. Hij lijkt in hem zijn definitieve beschermheer gevonden te hebben, al krijgt hij vermoedelijk nog steeds geen volledige financiële ondersteuning. In dit boek beschrijft hij diverse astronomische instrumenten die hij heeft bedacht zoals een equatorium, een hulpmiddel om de positie van planeten aan de hemel te bepalen.
In 1417 laat Ulūgh Beg in Samarkand, een stad in het zuidoosten van het huidige Oezbekistan, een wetenschappelijk instituut bouwen. Hij richt een ‘madrasah’ op, een soort universiteit. Dit instituut zou even later uitgroeien tot het centrum van de Islamitische wetenschappelijke wereld van de vijftiende eeuw. Honderden studenten zullen er in loop van de tijd les krijgen. In 1420 komt het gebouw gereed en tot de wetenschappers die Ulūgh Beg uitnodigt om er les te gaan geven behoort ook al-Kāshī. Vermoedelijk krijgt hij dan pas een volledige financiële ondersteuning van Ulūgh Beg, want in een brief aan zijn vader klaagt al-Kāshī: “[…] dat hij te laat is opgemerkt door de regering”.
In 1424 laat Ulūgh Beg – hij is zelf ook astronoom en doet allerlei onderzoeken – in Samarkand ook een groot observatorium bouwen om de sterrenhemel te kunnen bestuderen.
Een Russische postzegel uit 1987 met een portret van Ulūgh Beg en een tekening van zijn observatorium.
Het observatorium bestaat nog steeds. In 1908 worden de restanten er van terug gevonden en wordt het observatorium weer in volle glorie gerestaureerd.
Deel van een grote sextant in het gebouw met een lengte van liefst 63 meter en een kromtestraal van 40 meter, uitgelijnd op de lokale meridiaan. In de tijd van al-Kāshī zijn de muren met marmer bedekt, foto Wikipedia; Alaexis.
Dankzij de metingen gedaan in het observatorium trekt Ulug Bey de conclusie dat de aarde in 365 dagen, 5 uur, 49 minuten en 15 seconden om de zon draait, dat is slechts een afwijking van 30 seconden van “de moderne waarde” van een tropisch jaar (365 dagen, 5 uur, 48 minuten en 45 seconden). al-Kāshī is vanaf het begin ook werkzaam in het observatorium en is vermoedelijk zelfs de eerste president van observatorium.
Het jaar 1424 is ook het jaar, waarin het eerste grote wiskundige boek van al-Kāshī verschijnt. In dit werk geeft hij onder andere de waarde van 2π in zestien cijfers nauwkeurig achter de komma aan. Zijn (correcte) uitkomst luidt: 2π= 6.2831853071795865. Voor wie zich afvraagt waarom al-Kāshī er voor kiest om de waarde van 2π te berekenen en niet die van π, dat heeft te maken met de omtrek van een cirkel. Die is gelijk aan 2πr, waarbij r de straal van de cirkel is. Die zestien cijfers nauwkeurigheid van al- Kāshī is een aanmerkelijke verbetering van het oude ‘wereldrecord’ van zes cijfers nauwkeurigheid voor π.
(Even tussen haakjes, het zou tot 1596 duren voordat Ludolph van Ceulen, een Duits-Nederlandse wiskundige, dit record van 16 ‘goede cijfers’ zou verbeteren tot 32 stuks. Bij zijn dood in 1610 laat de vrouw van Van Ceulen op zijn grafsteen het getal π zelfs in 35 decimalen beitelen, wat wel wordt gezien als de eerste wetenschappelijke publicatie op een grafsteen. Omstreeks 1800 ging de oorspronkelijke grafsteen van Van Ceulen verloren, maar in juli 2000 onthulde toen nog prins Willem-Alexander op een pilaar in de Pieterskerk in Leiden een nieuwe gedenksteen waarop in een cirkel alle 35 cijfers van Van Ceulen te zien zijn.)
In 1427 verschijnt al-Kāshī beroemdste werk, ‘Miftāḥ al-ḥisāb’, dat ‘de sleutel van de rekenkunde’ betekent. Het is een leerboek voor zijn studenten waarin problemen aan de orde komen op het gebied van wiskunde, astronomie, bouwkunde en architectuur. Het is dit boek waarin al-Kāshī melding maakt van de decimale breuken (en de reden waarom hij samen met Simon Stevin postuum de Nobelprijs voor de Wiskunde krijgt). Eén van de hoofdstukken in het boek luidt: ’Over het rekenen met delen’. Al-Kāshī beschrijft hierin hoe je met decimale breuken moet rekenen.
In 1429 verschijnt zijn laatste wiskundige boek. Hierin berekent hij onder andere de sinus van een hoek van één graad. Zijn oplossing van sinus (1°) = 0.0174524064372835103712 is tot op 17 cijfers achter de komma nauwkeurig; pas bij het achttiende cijfer gaat het mis.
Datzelfde jaar, op 22 juni 1429 om precies te zijn, wordt hij vlakbij het observatorium in Samarkand vermoord. Sommige bronnen zeggen dat dit in opdracht was van Ulūgh Beg, zijn beschermheer. Dit omdat al-Kāshī weigert voor een rechtbank te verschijnen nadat hij kritiek geuit zou hebben op een aantal geestelijken. Maar zeker is dit niet en gezien het eerbetoon dat Ulūgh Beg hem na zijn dood brengt, kan je twijfels hebben of Ulūgh Beg bij zijn dood betrokken is. “…Een opmerkelijke wetenschapper, een van de beroemdste ter wereld, die de wetenschap van de oudheid perfect beheerste, die heeft bijgedragen aan de ontwikkeling ervan, en die de moeilijkste problemen kon oplossen.” laat Ulūgh Beg na de dood van al-Kāshī optekenen. Dit kan natuurlijk ook een gevalletje zijn ‘van de doden niets dan goeds’. Ulūgh Beg zelf zal overigens ook geen natuurlijke dood sterven. In 1449 wordt hij tijdens een pelgrimstocht naar Mekka vermoord, waarschijnlijk in opdracht van zijn oudste zoon. Van je familie moet je het maar hebben.
Er bestaan geen exemplaren meer van de ‘Miftāḥ al-ḥisāb’ uit 1427. Wel van een latere druk, waarvan in 1558 een exemplaar in Leiden opduikt. Wellicht is deze uitgave onder ogen gekomen van Simon Stevin en heeft hij hieruit zijn ideeën voor zijn ‘De Thiende’ gehaald. Het kan ook zijn dat Simon Stevin het boek niet kende en het idee van decimale breuken geheel zelfstandig opnieuw heeft bedacht.
21b Simon Stevin, 1548 – 1620; wetenschapper, zorgde voor de wereldwijde verspreiding van het idee van het systeem van decimale breuken.
Simon Stevin wordt in 1548 in Brugge geboren. Hij noemt zich zelf Simon Stevin van Brugghe. Hij is het buitenechtelijke kind van Antheunis Stevin en Catalyne van der Poort. Beiden behoren tot de betere kringen in Brugge. Zijn vader erkent het kind wel, maar ze trouwen niet. Zijn moeder voedt hem aanvankelijk alleen op. Later trouwt ze met de burgemeester van Brugge.
Simon heeft vermoedelijk een goede scholing gehad, maar waar hij die heeft genoten is niet bekend. Over de eerste dertig levensjaren van hem weten we niet veel. Hij is in ieder geval in Brugge en Antwerpen een tijd lang werkzaam in het financiële werkveld als kassier, klerk en boekhouder, niet echt opwindende beroepen. Ook onderneemt hij enkele reizen door Europa en verdiept zich tijdens die reizen (vermoedelijk) in de wetenschap.
In 1581 verhuist Simon Stevin – hij is dan 33 jaar oud; niet bepaald een wonderkind dus – naar de noordelijke Nederlanden. Hij vertrekt naar Leiden, waar hij gaat studeren en werken aan de door Willem van Oranje in 1575 gestichte Universiteit van Leiden. In 1581 en in 1582 publiceert hij er zijn eerste wetenschappelijke werken, ‘Nieuwe Inventie van Rekeninghe van Compaignie’ (Delft, 1581) en ‘Tafelen van Interest’ (Antwerpen, 1582). Het zijn boeken over geldbeheer, handelsrekenen en interesttafels. In 1583 publiceert hij in Leiden ook zijn eerste wiskundige boek: ‘Problemata geometrica‘ geheten.
Het zal niet zijn laatste boek zijn. Hij is een universele wetenschapper die op talrijke gebieden van de wetenschap actief is. Stevin is een veelschrijver. Zo publiceert hij boeken over de wiskunde, natuurkunde, hydraulica, astronomie, taal en de vestingbouw, met boektitels als ‘Wisconstighe Ghedachtenissen’, ‘De Beghinselen der Weeghconst, ’De Beghinselen des Waterwichts’, ‘De Hemelloop’ en ‘De Stercktenbouwing’. Voor de maritieme wereld is zijn boek ‘De Havenvinding’ over plaatsbepaling op zee van belang.
In 1585 publiceert hij zijn beroemdste boek ‘De Thiende’ – een pamflet van slechts 35 bladzijden. Het is dit werk waarin hij het rekenen met cijfers achter de komma beschrijft – “sonder ghebrokenen” zoals hij de breuken noemde.
Links het kaft; rechts een pagina uit het boek, waarin Stevin laat zien hoe je met decimale getallen kan rekenen.
Stevin maakt niet gebruik van een komma om aan te geven waar de decimale cijfers beginnen. In plaats daarvan laat hij alle getallen volgen door een cijfer in een cirkeltje, dat aangeeft door hoeveel veelvouden van tien het getal gedeeld moet worden. Als er een 1 in een cirkeltje achter een cijfer X staat, dan betekent dit dat getal X door tien moet worden gedeeld (in de huidige notatie is dit cijfer X het eerste cijfer achter de komma), een 2 in een kringetje houdt in delen door 10*10. Getallen met een 0 in een cirkeltje achter de cijfers zijn de gehele getallen ‘voor de komma’.
Neem bijvoorbeeld het getal 184,5429. Dat schrijft Stevin als volgt: 184 gevolgd door een 0 in een cirkel (de gehele getallen voor de komma dus); dan een 5 gevolgd door een 1 in een cirkel, dan een 4 met een 2 in de cirkel, vervolgens een 2 met daarachter het getal 3 in de cirkel en tot slot een 9 met een 4 in de cirkel. Bent u er nog? In de notatie van Simon Stevin ziet het getal 184,5429 er als volgt uit.
Het is niet echt een gemakkelijke schrijfwijze, die dan ook niet veel navolging krijgt.
In zijn boek laat Stevin ook zien hoe je met de ‘thiendes’ kan rekenen. Stevin schrijft het boek overigens niet als een theoretisch leerwerk voor collega-wetenschappers, maar vooral om aan het ‘gewone volk’ uit te leggen wat voor een voordelen het decimaal breukstelsel heeft. Wat hem betreft wordt een systeem met decimale breuken dan ook overal toegepast, hetgeen ook blijkt uit de groet die hij voorin in zijn boek plaatste: “Den Sterrekyckers, Landtmeters, Tapijtmeters, Wijnmeters, Lichaemmeters int ghemeene, Muntmeesters, ende allen Cooplieden, wenscht Simon Stevin Gheluck.”
Waar Stevin het idee van de ‘Thiendes’ vandaan heeft gehaald is niet bekend. Wellicht kent hij werk van al-Kāshī. Het kan ook zijn dat hij het idee “opnieuw uitvindt”. In het verleden gebeurt het wel vaker dat een bepaalde ontdekkingen in de loop van de tijd verloren gaan en opnieuw worden ‘uitgevonden’. Het boek van Stevin is in ieder geval een groot succes. Het wordt in meerdere talen vertaald en het is vooral aan zijn boek te danken dat het rekenen met decimale breuken een opmars door Europa maakt en Amerika populair wordt. Wel wordt zijn notatiewijze met cijfers in cirkeltjes al snel losgelaten en gaat men over naar een systeem met een decimale komma dan wel een decimale punt om aan te geven waar “de cijfers achter de komma” beginnen. Eén van de eersten die dit doet, is de Schot John Napier, de “bedenker” van de logaritme.
Een voorbeeld van de invloed van het boek van Stevin is in 1792 te zien. In dat jaar introduceert Thomas Jefferson de dollar in Amerika. Jefferson besluit om in tegenstelling tot het Engelse geldstelsel uit te gaan van een decimaal monetair stelsel. (Een dollar is op te delen in 10 dimes en 100 dollarcenten.) Hij heeft in 1780 het boek van Simon Stevin gelezen. In zijn verdediging van zijn voorstel om de dollar decimaal op te splitsen, verwijst hij dan ook naar ‘Disme, The Art of Tenths or Decimal Arithmetic. Invented by Simon Stevin’ (zo luidt de door Robert Norton in 1608 vertaalde Engelse uitgave van het boek van Stevin.) Het woord ‘disme’ vinden we ook terug op de eerste 10-centsstukken.
Een dime (een 10 centstuk) uit 1792; rechts de achterkant van de munt met daarop het woord ‘disme’; (disme is van oorsprong een Frans woord en betekent een tiende). Later verandert het woord ‘disme’ in ‘dime’. foto: National Numismatic Collection, National Museum of American History.
Naast ‘De Thiende’ is er nog een boek van Stevin dat nog steeds bekend is. Het betreft hier ‘De Beghinselen der Weeghconst’. Het verschijnt in 1586, een jaar na ‘De Thiende’.
In dit boek toont hij niet alleen aan dat een perpetuum mobile (een ‘zelfbeweger’ zoals Stevin een dergelijke apparaat noemt) niet kan bestaan. Ook beschrijft hij in het boek een experiment, waarmee hij aantoont dat Aristoteles ongelijk had toen deze stelde dat voorwerpen met een verschillend gewicht een verschillende valsnelheid zouden hebben.
Daartoe laat hij samen met zijn vriend Jan Cornets de Groot – de latere burgemeester van Delft (en vooral bekend geworden als de vader van Hugo de Groot – twee loden bollen (“twee loyen clooten”) van verschillend gewicht van de Nieuwe Kerk in Delft vallen om zo te bewijzen dat zware en lichte voorwerpen even snel vallen en tegelijkertijd de grond zullen raken. Deze proef wordt door sommige historici ook toegeschreven aan Galilei, die hem jaren later vanaf de Toren van Pisa zou hebben uitgevoerd. (Galilei vermeldt deze proef overigens niet zelf in zijn eigen geschriften). In elk geval zijn Stevin en De Groot voor zover bekend de eersten die een dergelijke experiment doen.
In tegenstelling tot veel van zijn tijdgenoten schrijft Stevin zijn boeken niet in het Latijn maar in het Nederlands. Hij vindt het Nederlands met zijn vele korte woorden, die allerlei mogelijkheden bieden om samenstellingen te maken, bij uitstek een geschikte taal om wetenschappelijke zaken te beschrijven. Bovendien vindt hij het belangrijk dat het gewone volk, dat geen Latijn kent, ook kennis kan nemen van wetenschappelijke werken. Of zoals hij het zelf zegt: “Ommedat al de werelt gheen Latijn can.” Onder het devies ‘een wonder is gheen wonder’ probeert hij voor leken op het oog onverklaarbare natuurfenomenen te verklaren. Simon Stevin introduceert in zijn boeken allerlei door hem bedachte nieuwe technisch-wetenschappelijke Nederlandse woorden. Zo hebben we in de Nederlandse taal de woorden wiskunde, scheikunde, vlak, evenaar, evenwijdig, loodrecht, vierkantswortel, middelpunt en raaklijn allemaal aan hem te danken.
Naast de valproef vanaf de kerk in Delft werkt Stevin ook op andere gebieden samen met Jan Cornets de Groot. Zo verbeteren ze, in opdracht van de stad Delft, een systeem van watermolens dat het water uit de polders rondom Delft moet reguleren – en dat ook, zeer belangrijk, de waterverplaatsingen ten behoeve van de Delftse brouwerijen moet verbeteren. Van Stevin is het idee om een aantal molens op korte afstand van elkaar te plaatsen, een zogenaamde molengang, waardoor het mogelijk is om het water verder omhoog weg te kunnen pompen.
Een molengang, drie molens op een rijtje in Leidschendam, oorspronkelijk aangelegd in 1672. Foto Marianne Spieker
Hij bedenkt daarnaast voor havensteden een methode om het verzanden van de havens te voorkomen. Hij maakt hierbij – naast het baggeren – gebruik van een speciaal systeem van sluizen waardoor het water snel weg kan stromen. Het snel wegstromende water neemt hierbij het zand mee. Hij schrijft hierover in zijn boek ‘Nieuwe Maniere van Sterctebou, door Spilsluysen’ (1617).
In de vaderlandse geschiedenisboeken komen we de naam Simon Stevin ook tegen. Hij is raadsman en leermeester van Prins Maurits. In 1593 treedt hij als adviseur in dienst bij de prins. Hij onderwijst hem niet alleen in de wiskunde maar is als ‘vernufteling’ – tegenwoordig zouden we ingenieur zeggen – ook betrokken bij de vestingbouw van Nederlandse steden. Zijn officiële titel luidt ‘kwartiermeester-generaal van het Staatse Leger’. Het is Stevin die in de strijd tegen de Spanjaarden de ideeën over vestingbouw, afkomstig uit Italië, onder de ogen van de prins brengt. Ook richt Stevin – het is een druk baasje – op verzoek van Prins Maurits aan de Universiteit van Leiden een ingenieursopleiding op, waar, en dat is vrij bijzonder, de lessen in het Nederlands (het toenmalige Nederduyts) worden gegeven.
Opmerkelijk genoeg is echter datgene waar de meeste mensen vandaag de dag Simon Stevin nog van kennen niet zijn boek over ‘de Thiende’ of één van zijn andere wetenschappelijke werken, maar van een door hem gebouwde zeilwagen. Het idee van een zeilwagen is niet nieuw. Ze bestonden al ten tijde van de Egyptische farao Amenemhat III – deze leefde zo’n 2000 jaar voor Christus. Maar het is Simon Stevin die als eerste in Europa een groot exemplaar bouwt. Hij doet dit in 1602 in opdracht van Prins Maurits.
Het is een grote wagen met aan boord plaats voor zo’n dertig mensen. In februari 1602 maakt de zeilwagen onder grote belangstelling zijn eerste rit over het strand van Scheveningen naar Petten. Prins Maurits staat zelf aan het stuur. Aan boord bevindt zich ook de dan 19-jarige Hugo de Groot die een lang gedicht over de tocht en schipper Prins Maurits zal schrijven. “Die t’Vaderlandt beschermt / de doot sijns Vaders wreeckt, / In t’Ooste werdt geeert, / en werdt gevreest in t’Weste, / Die ist die nu bezeylt des groote Waters veste,/ Daer hy het Hollandsch strandt met sijne wielen breeckt.”
Ook aan boord bevindt zich de Spaanse admiraal Francisco Mendoza, die zes maanden eerder krijgsgevangen is gemaakt tijdens de slag bij Nieuwpoort. Een half jaar later zal Mendoza worden uitgewisseld tegen 400 door de Spanjaarden krijgsgevangen genomen zeelieden, onder wie Piet Hein. Deze zal Mendoza 25 jaar later diens zilvervloot afpakken. Over de afstand van zo’n 80 km zou de zeilwagen twee uur hebben gedaan, wat inhoudt dat hij met een gemiddelde snelheid van zo’n 40 km per uur over het strand moet hebben gereden. Of dit waar is, weten we niet.
Volgen de volksoverlevering stuurt Prins Maurits de wagen, om zijn gasten even wat schrik aan te jagen, kortstondig de zee in. “Eenmaal, tot kortswijl en om den Heeren een pots te doen, stierde sijn Excellentie de Wagen in Zee, waerover vele sich dapper ontzetteden; maar subijt het roer gewent zijnde, quam de Wagen weer op strandt en vloot sijn oude koers.” aldus een ooggetuigenverslag (zoals geciteerd door E. Dijksterhuis in diens boek over Simon Stevin uit 1943)
De wagen blijft nog bijna 200 jaar in gebruik bij de Oranjes, maar na de Franse bezetting in 1795 wordt de wagen geveild. Een Scheveningse visser koopt de wagen, maar als de schuur waarin de zeilwagen staat in 1811 in elkaar stort, raakt de wagen zwaar beschadigd en sloopt de visser de wagen.
In 1612 verhuist Simon Stevin van Delft naar Den Haag en laat er een huis bouwen aan de Raamstraat 47. Hier woont hij (ongetrouwd) samen met een zekere Catherina Craij. In 1616 – ze hebben dan al drie kinderen – trouwen ze alsnog. Een jaar later zal er nog een vierde kind volgen. In 1620 overlijdt Simon Stevin, de man die er voor zorgde dat het idee van decimale breuken wereldwijd bekend raakt, op 70-jarige leeftijd in Den Haag.
Tot slot, in 1960 ontwerpt Philips een computer die ze ter ere van Simon Stevin de naam STEVIN geven. Die afkorting staat voor “Snel Tel En Vermenigvuldig INstrument”. De STEVIN wordt overigens tegelijk gebouwd met de PASCAL. Dat staat voor Philips Akelig Snelle CALculator.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie