Een wiskundige grap: “Er zijn 10 soorten mensen: Mensen die binair kunnen tellen en mensen die dat niet kunnen.” Normaal gesproken is het niet zo’n goed teken als je een grap moet uitleggen, maar laat ik dat in dit geval toch maar even doen. De grap is namelijk dat het getal ‘10’ in het binaire stelsel gelijk is aan het getal twee in het decimale getallenstelsel.
In het binaire getallenstelsel worden alle getallen met alleen maar nullen en enen geschreven. De eerste twee getallen van het decimale en het binaire systeem zijn nog het zelfde (het decimale getal 0 is gelijk aan het binaire getal 0 en 1 = 1) maar daarna gaan ze verschillen: 2 = 10; 3 = 11; 4 = 100; 5 = 101; 6 = 110; 7 = 111; 8 = 1000; 9 = 1001 en 10 = 1010; enzovoorts, enzovoorts. (In de binaire wereld geldt dus 1 + 1 = 10)
Het aantal nullen en enen bij binaire getallen loopt snel op; neem het decimale getal 1234, dat is binair gelijk aan 10011010010. Maar omdat er alleen sprake is van enen en nullen is het binaire getallenstelsel wel een zeer geschikt getallensysteem voor computers om mee te werken. Een schakelaartje aan of uit, wel of geen lichtflitsje, wel of niet een stroomstootje. Er zijn vele manieren om een computer te laten weten of een bepaalde waarde 0 of 1 moet zijn.
Eén van de allereerste mensen die een systeem met binaire waardes beschreef, was 2200 jaar geleden een Indiër, een zekere Pingala. Daarvoor waren er ongetwijfeld ook al mensen die zich met binaire getallensystemen bezig hielden, maar Pingala was de eerste die zijn gedachten hierover op papier zette. Nou ja, op papier, op papyrus dus want papier bestond nog niet in de tijd van Pingala. Hij deed dat ongeveer 200 jaar voor Christus in zijn ‘Chandah-shāstra’, een boekwerk dat vooral ging over taal (het Sanskriet) en het gebruik van het metrum in versregels.
Om zijn ideeën hierover uit te leggen bedacht hij een telsysteem dat gebruik maakte van de klankduur van woorden – dat wil zeggen de tijd die nodig is om een woord uit te spreken. Zijn ‘teleenheid’, de klankduur, kon twee waarden hebben: ‘kort’ of ‘lang’. (Te vergelijken met de waardes 0 en 1 bij een binair getallenstelsel). Daarom kan men het klanksysteem van Pingala beschouwen als een binair systeem.
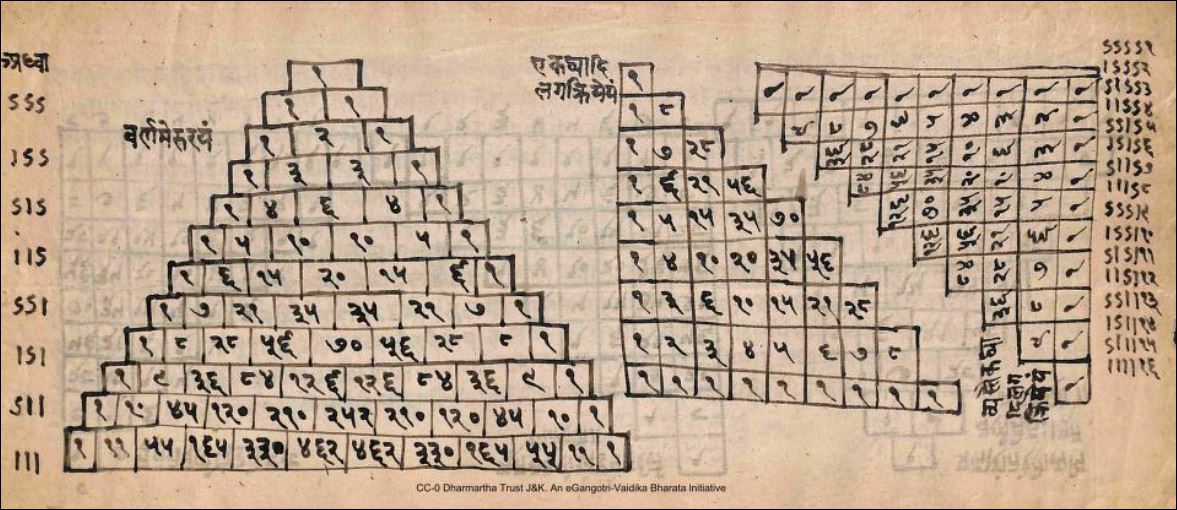
 Pagina met daarop het werk van Pingala; dit manuscript stamt uit 755 na Christus: Bron: Prakrit Pingala Prastara; Raghunath Temple, Jammu, Library J&K;
Pagina met daarop het werk van Pingala; dit manuscript stamt uit 755 na Christus: Bron: Prakrit Pingala Prastara; Raghunath Temple, Jammu, Library J&K;
Hoewel het werk van Pingala taalkundig gericht is, bevat het ook een aantal “wiskundige” analyses over het aantal mogelijke combinaties van klankduren. Eén van deze analyses heeft als uitkomst een getallenreeks, die tegenwoordig bekend staat als de ‘getallenrij van Fibonacci’. Dit omdat de reeks “voor het eerst” opduikt in een boek van de Italiaan Fibonacci uit 1202. Omdat niemand in de wiskunde, inclusief Fibonacci zelf, op dat moment weet dat een zekere Pingala 1400 jaar eerder – nota bene in een boek over taal – ook al een dergelijke rij heeft beschreven, krijgt de getallenrij de naam de rij van Fibonacci en niet de rij van Pingala.
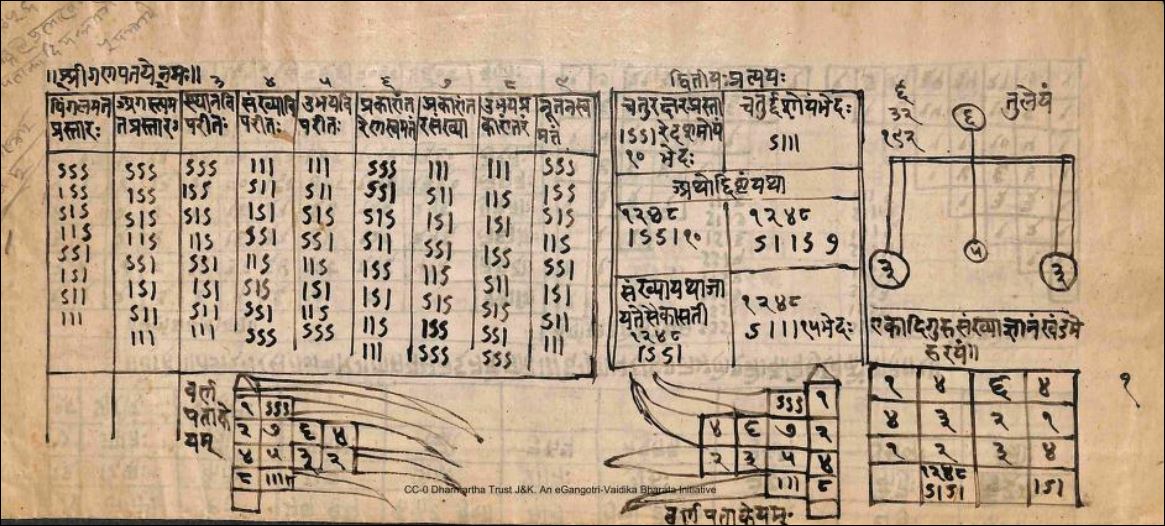
Hetzelfde zien we met de zogeheten driehoek van Pascal. Ook hier geldt dat Pingala al eeuwen eerder iets soortgelijks liet zien. Eigenlijk zou de driehoek van Pascal dus de driehoek van Pingala moeten heten.
Pingala’s driehoek van Pascal; Bron: Prakrit Pingala Prastara; Raghunath Temple, Jammu, Library J&K;
Ook wordt Pingala zijn naam wel eens genoemd in verband met morsecode, dit omdat in morse letters, cijfers en leestekens met combinaties van korte en lange klankduren worden aangegeven (SOS: kort kort kort, lang lang lang, kort kort kort), maar dat is wat te veel eer. Pingala zond nooit een SOS-signaal uit.
Wie was Pingala?
Wanneer en waar Pingala precies heeft geleefd is onbekend. De meeste bronnen plaatsen hem ergens in het India van de tweede eeuw voor Christus. Er zijn echter ook verhalen dat hij een broer van een zekere Panini zou zijn. Een naam die we tegenwoordig kennen van de voetbalplaatjes en de broodjes, maar deze Panini leefde in de vierde eeuw voor Christus en hield zich vooral bezig met het Sanskriet, de taal die in India werd gebruikt voor filosofische en religieuze geschriften. Het is onder andere de taal van het boeddhisme en hindoeïsme.
 Voorbeeld van een tekst in het Sanskriet uit de elfde eeuw; foto Wikipedia
Voorbeeld van een tekst in het Sanskriet uit de elfde eeuw; foto Wikipedia
Als Pingala inderdaad de broer van Panini zou zijn geweest, dan zou Pingala dus twee eeuwen eerder hebben geleefd (in ca. 400 voor Christus) dan algemeen wordt aangenomen, maar hoogstwaarschijnlijk moeten we dat ‘broer zijn’ zien in overdrachtelijke zin. Waarschijnlijk wordt er mee bedoeld dat Pingala net zoals Panini zich met taal bezig hield. De meeste deskundigen houden het er op dat Pingala ca. 200 jaar voor Christus leefde. Veel meer over de persoon Pingala weten we echter niet, wel over zijn werken.
Hij houdt zich bezig met mantra’s (dat zijn gedichten en uitspraken in de vorm van spreuken of gebeden) in het Sanskriet. In het bijzonder houdt hij zich bezig met de klankduur en met de prosodie van de mantra’s. Dat laatste klinkt moeilijk. Ik citeer nu maar even de Wikipedia:
“Prosodie is in de fonologie het ritme, de klemtoon en de intonatie van de stem bij het uitspreken van een zin of zinsdeel (in tegenstelling tot kleinere elementen als woorden en morfemen). Dit kan bijvoorbeeld te maken hebben met verschillende eigenschappen van de spreker die in de uiting van een zin zijn te horen. Prosodie kan bijvoorbeeld meer informatie verschaffen omtrent de emotionele toestand waarin de spreker verkeert, of een zin bedoeld is als vraag of als opmerking, of de spreker serieus is of juist ironisch, en andere elementen van een taal die niet worden ondersteund door grammatica of de woordkeuze.”
Zo, bent u er nog? We zijn nu behoorlijk ver verwijderd van het binaire getallenstelsel, maar we gaan vanaf nu die kant op. Pingala onderscheidt namelijk twee soorten klanken: korte en lange klanken. Een simpel voorbeeldje in het Nederlands. Neem de woorden ‘knie’ en ‘jaar’, allebei zijn het éénlettergreep-woorden van vier letters groot. Echter doordat de combinatie ‘ie’ in knie veel korter wordt uitgesproken dan die dubbele ‘aa’ in jaar hebben ze een verschillende klankduur. Probeert u het maar eens uit: een ‘jaar’ duurt langer.
Pingala is van mening dat versregels een bepaald metrum moeten hebben en om te kijken of ze dat metrum hebben deelt hij woorden (of delen van woorden) in twee categorieën in: woorden (of woorddelen) met een korte klankduur en woorden (of woorddelen) met een lange klankduur. De korte klankduur is hierbij de basis van zijn metrum-systeem. De lange klankduur stelt hij ongeveer gelijk aan twee keer de korte klankduur. Pingala heeft een voorkeur voor vijf types versregels: a) regels met vier korte klanken; b) regels met één lange klank en drie korte klanken; c) regels met twee lange en twee korte klanken; d) regels met drie lange klanken en e) regels met één korte klank en vier lange klanken.
Hij maakt allerlei analyses ten aanzien van het aantal klanken in versregels en schrijft hierover in zijn boekwerk ‘Chandah-shāstra’ (‘kunst van de versmaat’). De Chandaḥ-shāstra is een werk van acht hoofdstukken. Hij beschrijft hierin ook hoeveel verschillende combinaties van lange en korte klanken er mogelijk zijn bij een bepaalde klankduur van een versregel.
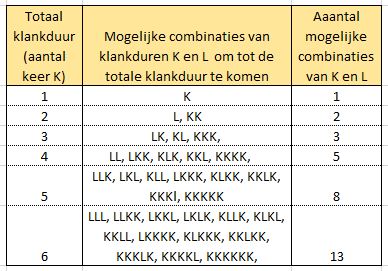
Zie bijvoorbeeld onderstaande tabel. (In de eerste kolom staat de totaal klankduur van een bepaalde versregel, in de twee kolom staan de mogelijke combinaties van lange en korte klanken die leiden tot deze klankduur. Hierbij staat K voor een korte klankduur en L voor een lange klankduur. (L is 2 keer zo lang als K.) In de derde kolom staat ten slotte aangegeven hoeveel verschillende combinaties van K en L er zijn die leiden tot de gewenste totale klankduur. Zo zijn er bijvoorbeeld acht verschillende combinaties van K’s en L’s mogelijk om te komen tot een versregel van vijf klanken.)
Aangezien zijn klankduren maar twee waardes (‘kort’ of ‘lang’) kunnen hebben, kan je zijn systeem zien als het allereerste beschreven binaire stelsel, waarmee hij zijn plaats heeft verdiend in het overzicht van mensen achter de computer. Wel geldt dat zijn systeem behoorlijk afwijkt van het huidige binaire getallensysteem. Zo bevat zijn systeem geen waarde ‘nul’. Een versregel met nul klanken is immers geen versregel. Ten opzichte van het “normale” binaire stelsel geldt verder dat Pingala zijn klankwaarde-systeem van links naar rechts opbouwde, terwijl dat in het binaire getallensysteem van rechts naar links geschiedt. Ook konden in het systeem van Pingala meerdere combinaties dezelfde uitkomst hebben, bijvoorbeeld LL = KKKK. Zoiets kan in het binaire systeem met de getallen 0 en 1 absoluut niet.
Het werk van Pingala is niet alleen bekend geworden vanwege zijn opzet voor een binair systeem. Wie namelijk goed kijkt naar de rechterkolom van voorgaande tabel ziet daar de reeks 1, 2, 3, 5, 8, 13, … staan. De wiskundigen herkennen hierin direct de getallenreeks van Fibonacci. In deze getallenrij is het getal N steeds gelijk aan de som van de twee voorgaande getallen. Leonardo van Pisa, bijgenaamd Fibonacci, kwam met deze rij op te proppen in zijn boek ‘Liber abaci’ uit 1202, maar Pingala was hem dus eigenlijk 1400 jaar voor. Alleen raakte diens werk in de vergetelheid.
Veel wiskundig nut heeft de reeks niet, maar wel op het gebied van de schoonheid. Deel je namelijk telkens een getal uit de Fibonaccireeks door zijn voorganger uit de reeks, dat zal de uitkomst van deze deling steeds meer het gulden-snede-getal benaderen. Hoe verder je in de reeks komt, hoe beter die benadering. De gulden snede verhouding. meestal aangeduid met de Griekse letter φ (phi), is ongeveer 1,6 staat tot 1.
Deze verhouding vindt je vaak terug in allerlei vlakverdelingen – het ene vlak is dan 1,6 keer zo groot als het andere vlak. Mensen schijnen dit een prettige verhouding te vinden. Je ziet deze verhouding dan ook terug in allerlei zaken. Bijvoorbeeld bij een vlakverdeling van schilderijen, maar ook in de natuur, bijvoorbeeld bij schelpen en de wijze waarop de zaden van een zonnebloem zijn gerangschikt.
 Een schelp met gulden snede verhoudingen. (This Wikipedia and Wikimedia Commons image is from the user Chris 73 and is freely available under the creative commons cc-by-sa 3.0 license.)
Een schelp met gulden snede verhoudingen. (This Wikipedia and Wikimedia Commons image is from the user Chris 73 and is freely available under the creative commons cc-by-sa 3.0 license.)
Nog een schelp met gulden snede verhoudingen: de ‘Geboorte van Venus’, een schilderij van de Italiaanse kunstschilder Sandro Botticelli.
In dit geval zit de gulden snede verhouding niet in de schelp, maar in de lengte-breedte verhouding van het schilderij.
Tot slot, Pingala wordt ook wel eens in verband gebracht met morsecode. Dit omdat de morsetekens bestaan uit combinaties van korte en lange klanken. De keuze daarvoor heeft echter niks met Pingala’s klankduren te maken. De marconist van de Titanic was dan ook niet geïnteresseerd in een mooi metrum in zijn berichten maar in schepen die te hulp konden snellen.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie