De in 2014 overleden Hugo Brandt Corstius zei ooit eens: “Eén ding zal de computer nooit kunnen: van de apen afstammen.” Dat had hij fout gezien. De allereerste ‘computer’ bestond namelijk uit twee bavianenbotjes, waar een onbekend gebleven persoon streepjes in kerfde, waardoor deze botten als telstokjes konden worden gebruikt. Deze zogenaamde Ishango-beentjes staan te boek als het oudst bekende hulpmiddel van de mens om te kunnen rekenen.
Eén van de zaken waarin de mens zich van dieren onderscheidt, is dat de mens kan rekenen en dieren niet. Hoewel, begin vorige eeuw was daar opeens ‘Kluger Hans’, een paard in Duitsland dat getallen kon herkennen en er zelfs mee kon rekenen. Zijn eigenaar, Wilhelm von Osten, een leraar aan een gymnasium, had hem dit geleerd. Door met zijn voorbeen op de grond te tikken gaf het paard de uitkomst van een berekening aan. Vroeg men bijvoorbeeld aan Kluger Hans hoeveel 3×4 was, dan tikte het paard 12 keer op de grond. Hij kon zelfs worteltrekken.
 Kluger Hans, Wilhelm von Osten, en Kluger Hans onder veel belangstelling aan het rekenen.
Kluger Hans, Wilhelm von Osten, en Kluger Hans onder veel belangstelling aan het rekenen.
 Hier krijgt Kluger Hans de opgave 4+2 voorgelegd.
Hier krijgt Kluger Hans de opgave 4+2 voorgelegd.
Aanvankelijk dacht men dat er sprake van bedrog moest zijn. Op de een of andere wijze zou Von Osten het paard een seintje geven hoe vaak hij op de grond moest tikken, vermoedelijk door de opgaven op een bepaalde stemhoogte uit te spreken. Maar toen Kluger Hans ook bleek te kunnen “rekenen” als Von Osten niets zei en het paard alleen de sommen op een schoolbord of op papier liet zien, besloot men in 1904 om een wetenschappelijke commissie aan het werk te zetten om het fenomeen van het paard dat kon rekenen nader te onderzoeken.
 Kluger Hans wordt getest. Enkele leden van de commissie aan het werk; rechts daarvan Von Osten.
Kluger Hans wordt getest. Enkele leden van de commissie aan het werk; rechts daarvan Von Osten.
De commissie werd aangevoerd door een professor in de psychologie, verder zaten een circusdirecteur en een goochelaar in de commissie om te kijken of Von Osten toch niet een of andere truc uithaalde. Men kon echter niks ontdekken en het leek er warempel op dat het paard daadwerkelijk getallen kon herkennen en kon rekenen.
 Er werd ook getest of Kluger Hans met een soort typemachine woorden kon maken, maar dat lukte niet.
Er werd ook getest of Kluger Hans met een soort typemachine woorden kon maken, maar dat lukte niet.
Er werd een tweede onderzoeksgroep ingesteld die een uitgebreider onderzoek ging doen. Na een tijdje ontdekte deze commissie dat hoe verder Kluger Hans van Von Osten afstond hoe slechter hij ging rekenen en als het paard oogkleppen op kreeg, dan bakte hij er zelfs helemaal niks meer van. Ook viel het op dat als Von Osten de opgave zag, dat dan Kluger Hans in 98% van de gevallen het goede antwoord gaf. Zag Von Osten daarentegen de opgave zelf niet – en hield hij het paard een aangereikt bordje of papier met de rekensom voor, zonder dat hij de opgave zelf kon lezen, dan zakte het percentage goede antwoorden van Kluger Hans naar slechts 8,5%.
Wat bleek, Kluger Hans had zichzelf aangeleerd – hij kreeg altijd een stukje wortel als beloning als hij het goede antwoord gaf – om de lichaamstaal van Von Osten en van mensen in zijn omgeving te herkennen. Als Von Osten – hij dacht echt dat zijn paard kon rekenen – of mensen in zijn omgeving, na het stellen van een vraag bijvoorbeeld iets omlaag keken om te zien of het paard met zijn been ging tellen, dan herkende Kluger Hans deze lichaamsbeweging en begon hij met zijn been te tikken. En kwam het paard bij het goede antwoord en bewogen Von Osten of de mensen om hem heen hun hoofd (of slechts hun ogen) iets omhoog om te zien of het paard zou stoppen, dan herkende Kluger Hans ook deze beweging en hield hij op met tikken.
Kluger Hans was inderdaad een slim paard. Hij had geleerd lichaamstaal te herkennen, heel knap, maar rekenen, nee dat kon hij niet. Tegenwoordig noemt men in de wetenschap dit effect – dat een ondervrager onbewust de ondervraagde het gewenste antwoord aanreikt – het Clever Hans Effect, iets waarop men bijvoorbeeld bedacht moet zijn bij het ondervragen van getuigen.
Even tussendoor, rekenen kunnen dieren niet maar een beetje “tellen” schijnen sommige dieren wel te kunnen. Zo is er een vogelsoort dat altijd een nest met vier eieren legt. Haalt men twee eieren weg, dan zal het beest er twee bij leggen, haalt men er één weg, dan legt hij er maar eentje bij. Ook zijn er onderzoeken, waaruit blijkt dat apen een rudimentair besef voor getallen hebben. Zo verscheen er in Science in 2002 een artikel waarin melding werd gemaakt dat de apen in hun hersenschors neuronen hebben die gevoelig zijn voor een bepaald getal. Veel hoger dan vijf komen de apen echter meestal niet, en dat laatste getal sluit dan weer mooi aan bij het fraaie ‘urban legend’ verhaal van de Amerikaanse boer die last had van een kraai die op zijn graanzolder nestelde.
De boer wou de kraai daar weg hebben, maar als de boer de ladder naar de hooizolder op klom om hem te vangen, dan vloog de kraai weg en ging hij buiten in een boom zitten wachten totdat de boer weer de ladder afdaalde. Op een dag had de boer een plan bedacht. Hij ging samen met een knecht de hooizolder op. Hij ging daarna weer met de trap omlaag maar liet de knecht op de hooizolder achter. De kraai bleef echter in de boom zitten wachten totdat ook de knecht de ladder was afgedaald. De volgende dag probeerde de boer het met twee knechten – hijzelf en één van de knechten daalde met hem af; de andere bleef zitten – maar ook dat hielp niet. Pas toen ze alle drie weer beneden waren vloog de kraai weer naar de hooizolder. Idem dito toen de boer het daarna met drie en vier knechten probeerde – het was een komen en gaan van knechten. Pas toen de boer met vijf knechten de zolder opging, raakte de kraai de tel kwijt. Toen de boer en vier knechten waren afgedaald, vloog de kraai terug naar de hooizolder en kon de vijfde knecht het beest pakken. De kraai kon blijkbaar niet verder dan vijf tellen.
Een tellende kraai
Ook vermeldenswaardig is Koko de Gorilla, geboren in de dierentuin van San Francisco maar die bijna zijn hele leven (1971-2018) verbleef in ‘The Gorilla Foundation’’ in Woodside, Californië. Haar verzorgster stelde dat Koko meer dan 1000 tekens in gebarentaal kende en ook dat ze de betekenis van 2000 Engelse woorden begreep, waardoor er een soort van primitieve conversatie met haar mogelijk was.
Opmerkelijk was dat Koko blijkbaar ook een soort fixatie op tepels had, zowel van mannen als van vrouwen. Iets wat ze met haar gebarentaal aangaf. Dat leidde in 2005 tot een rechtszaak toen twee vrouwelijke medewerksters van het instituut de verzorgster van Koko beschuldigden dat deze hen meerdere malen verzocht om hun borsten voor Koko te ontbloten, zodat Koko er naar kon kijken. Ze eisten een miljoen dollar schadevergoeding. De zaak werd uiteindelijk buiten de rechtszaal geschikt. Maar nu zijn we wel heel ver afgedwaald
Maar goed, mensen kunnen dus wel verder dan vijf tellen en ook met getallen rekenen. Wel vindt men het rekenen soms lastig, zeker als er sprake is van ingewikkelde berekeningen. Dan wordt er vaak gebruik gemaakt van hulpmiddelen. Soms is dat alleen een pen en papier, maar het kan ook een telraam, een rekenmachine of een computer zijn. In de oudheid moest men het echter met primitievere hulpmiddelen doen. De oudste gevonden hulpmiddelen zijn twee bavianenbotjes met daarin streepjes gekerfd.
 Twee zijden van het eerste Ishango-bot
Twee zijden van het eerste Ishango-bot
De botten zijn in 1950 door de Belgische geoloog Jean de Heinzelin gevonden bij Ishango, een plaats in het huidige Democratische Republiek Congo (het vroegere Belgische Congo), gelegen aan de grens met Uganda. Op deze plek bevond zich vroeger een nederzetting, die op een gegeven moment werd bedolven door de as van een vulkanische uitbarsting.

 Jean de Heinzelin omstreeks 1941; (foto Wikipedia) en een pagina uit het oorspronkelijke onderzoeksverslag met afbeeldingen van de vindplaats.
Jean de Heinzelin omstreeks 1941; (foto Wikipedia) en een pagina uit het oorspronkelijke onderzoeksverslag met afbeeldingen van de vindplaats.
De Heinzelin, een onderzoeker aan het Koninklijk Belgisch Instituut voor Natuurwetenschappen, voert in 1950 in het toenmalige ‘Nationaal Albert Park’, in opdracht van de voormalige Belgische overheidsdienst ‘Nationale Belgische Parken in Afrika’ opgravingen uit. In 1935 waren in dit park al visserswerktuigen gemaakt van dierenbotten, bewerkte kwartsstukjes en een mensachtige kaak ontdekt. De Heinzelin vindt in 1950 in een aardlaag bij de oever van de Semliki, ter hoogte van de plaats waar deze rivier het Edward-meer uitstroomt, twee botjes met daarin strepen gekrast. Behalve de botten worden er op deze plek ook honderden andere voorwerpen gevonden.
Het duurt even voordat er een verslag verschijnt van de expeditie maar in 1955 is het zover. In dat jaar verschijnt het eerste verslag van de expeditie, gevolgd door een tweede verslag in 1957. (In totaal zullen er nog vier verslagen volgen.) In het eerste verslag komt de vondst van het bekraste bot slechts één keer terloops aan de orde. Op pagina 65 wordt een botje met inkepingen terloops als één van de vondsten vermeld.
Twee jaar later is dit wel anders. In dit verslag wordt uitgebreid ingegaan op de vondst. De Heinzelin besteedt dan een heel hoofdstuk aan het bot met de kerven.
Links het kaft van het rapport uit 1957; rechts: Het oudste terug gevonden rekenhulpmiddel van de mens: één van de twee Ishango botjes zoals deze nu te zien is in het Museum voor Natuurwetenschappen in Brussel. Duidelijk zichtbaar zijn de strepen. Het Ishango-been lag voordat het een prominente plaats in het museum kreeg jarenlang weggeborgen in een lade van het museum. Het botje is ongeveer 10 cm lang. Boven in de punt zit een bewerkt kwartskristal. Foto botje: Ben2; Wikipedia
Volgens een onderzoek, gedaan met behulp van de koolstof-14 methode, zijn de botten ongeveer 22.000 jaar oud. Nu zijn er weliswaar ook andere oude botten gevonden waarin streepjes zijn gekerfd – bijvoorbeeld een 30.000 jaar oud wolvenbot met 55 streepjes dat gevonden is bij Věstonice in het huidige Tsjechië; en een bot van 35.000 jaar oud dat in Swaziland is gevonden met daarin 29 krassen – maar bij geen van deze botten lijkt er enige logica in de situering van de streepjes op het bot te zitten en lijken ze niet bedoeld om er mee te rekenen.
 Het 30.000 jaar oude Wolvenbot gevonden in Tsjechië
Het 30.000 jaar oude Wolvenbot gevonden in Tsjechië
 Het 35.000 jaar oude bot dat is gevonden in Swaziland
Het 35.000 jaar oude bot dat is gevonden in Swaziland
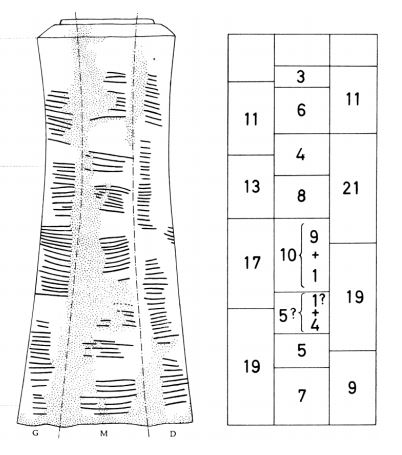
Bij het Ishango-bot lijkt er echter wel een logica in de situering van de streepjes op het bot te zitten. Op het bot staan drie kolommen met streepjes, die elk in verschillende groepen zijn verdeeld. De verdeling van de streepjes, ziet er als volgt uit (rechts staan de aantallen streepjes opgeteld per groep weergegeven):
Figuren afkomstig uit het originele verslag van De Heinzelin uit 1957
In de eerste kolom staan de priemgetallen tussen 10 en 20. Deze kolom telt op tot 60. Ook de derde kolom telt op tot zestig. De middelste kolom ziet er wat ingewikkelder uit. Er staan een aantal priemgetallen (3, 5 en 7) en verdubbelingen op (3->6; 4->8). De streepjes van deze kolom tellen samen op tot 48.
De Heinzelin vermeldt in zijn tweede verslag meer rekenkundige verbanden. Uit zijn tweede verslag uit 1957 (hierbij staan de namen Ma, Mb enzovoorts voor de hoeveelheid streepjes in een bepaalde groep):
Je kan je afvragen of De Heinzelin hier niet wat meer ziet, dan dat degene die de strepen in het bot heeft gekrast heeft bedoeld.
Het is overigens niet helemaal zeker of de botten inderdaad een rekenhulpmiddel zijn, In de loop van de tijd zijn er verschillende andere verklaringen bedacht voor deze streepjes. Volgens sommigen vormen de streepjes een maankalender, volgens anderen is het een rekenspel om kinderen te leren rekenen en weer anderen zien er een combinatie van rekenhulpmiddelen in. Ook de mogelijkheden van een kerfstok, een instrument om de visvangst te verdelen, een godsdienstig voorwerp en een bijgehouden menstruatiecyclus zijn genoemd. Het kunnen natuurlijk ook gewoon willekeurige krassen zijn van iemand die zich 22.000 jaar geleden verveelde.
In 1998 onthulde De Heinzelin, vlak voordat hij overleed, dat er nog een tweede botje met krassen was gevonden. De aanwezigheid daarvan had hij altijd verzwegen, vermoedelijk omdat hij na zijn vondst en de publicatie over het eerste botje en zijn theorieën over de streepjes veel kritiek had gekregen. Dit tweede botje is 14 cm lang. Het is wat lichter van kleur, gepolijst en hol van binnen. Op dit bot staan zes kolommen met 90 krasstrepen, veelal in groepen van zes. Sommige van die kerven zijn groot, anderen klein. De verdeling van de strepen over dit bot is niet zo opvallend als die van het eerste bot. Zo zijn er bijvoorbeeld geen priemgetallen in te herkennen.
In de jaren na het overlijden van De Heinzelin is ook dit tweede bot uitgebreid onderzocht. Volgens onder andere de Belgische wiskundige Dirk Huylebrouck vormen de twee botten samen waarschijnlijk een rekenhulpmiddel in de vorm van rekenstokjes. Als die veronderstelling klopt, dan zouden de Ishango-beenderen daarmee gelden als het oudste hulpmiddel van de mens om te kunnen rekenen.
Hoe je met de botjes moet rekenen en in welk getallenstelsel is onbekend. De twee beentjes zouden telstokken kunnen zijn van een volk dat niet decimaal telde en rekende, maar dit deed met de teleenheden 6 en 10. Maar ook een 12-tallig en een 60-tallig getallenstelsel zijn als mogelijkheid geopperd. (Voor wie zich afvraagt waarvoor je een 60-tallig getallenstelsel zou kunnen gebruiken, denk aan de tijd, waarbij een uur is verdeeld in 60 minuten en een minuut in 60 seconden.)
Het is dus nog steeds onbekend hoe men de strepen op de botten moet interpreteren. Maar in ieder geval niet als een streepjescode om te scannen, zoals wel gebeurde bij deze postzegel.
Belgische postzegel – ontwerpster Clothilde Olyff – uitgegeven in 2000 ter gelegenheid van het internationale jaar van de wiskunde; De streepjes onderaan de postzegel stellen de Ishango-streepjes voor (een 3 en een 6), maar werden door sommige winkeliers aangezien voor een nieuw soort streepjescode. Ze probeerden tevergeefs om de postzegels te scannen.
Wie de streepjes in de botten heeft gekrast is uiteraard onbekend. Er leefde 22.000 jaar geleden in deze omgeving een volk dat zich onder andere met landbouw en visserij bezig hield. Zo zijn er maalstenen en vijzelstampers gevonden, evenals van stenen gemaakte weerhaakjes en veel benen harpoenen. Het zou kunnen dat dit volk behoorde tot de Batwa-pygmeeën maar dat is niet zeker. Maar als dat zo is, en de stokjes zijn inderdaad een rekenhulpmiddel, dan is de verleiding nu wel erg groot om te schrijven: ‘kleine mensen, grote ideeën’.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie