Computers leven van enen en nullen. Ok, ook een beetje van stroom en algoritmes (instructies) maar verder draait het bij een computer toch vooral om enen en nullen.
Het getal nul is één van de belangrijkste getallen in de wiskunde die er bestaan. Daarom is het eigenlijk een beetje wonderlijk dat pas in de zevende eeuw na Christus iemand met een definitie voor het getal nul komt en rekenregels opstelt hoe er met het getal nul gerekend moet worden. Alle wereldrijken daarvoor zoals het Oud-Perzische Rijk, de Grieken (kenden wel de stelling van Pythagoras maar hadden geen getal 0); en het Romeinse rijk kwamen op en gingen ten onder zonder dat ze over rekenregels met betrekking tot het getal nul beschikten. Misschien gingen ze daarom wel ten onder.
Als men u deze klok probeert te verkopen als een originele tweeduizend jaar oude Romeinse klok, trap er niet in! De Romeinen kenden niet het cijfer 0. foto Philip James
De persoon die als eerste het getal nul definieert en er rekenregels voor bedenkt, is Brahmagupta. Hij leefde van 598 – 668 in wat nu India is en was een wiskundige en astronoom. Hij schrijft voor het eerst over het getal nul in zijn boek Brahma-sphuta-siddhanta dat in 628 verschijnt. Brahmagupta schrijft in dat boek niet alleen over het getal nul, maar geeft ook rekenregels hoe men met negatieve getallen moet rekenen.
Ook schrijft hij in dat boek kort over de zwaartekracht. Die beschouwt hij als een aantrekkingskracht; “De Aarde is aan al haar kanten hetzelfde; alle mensen op Aarde staan rechtop, en alle zware dingen vallen op de Aarde door een natuurwet, want het is de aard van de Aarde om dingen aan te trekken en vast te houden, zoals het de aard van water is om te stromen… […] zaden keren er altijd naar terug, in welke richting je ze ook weggooit, en komen nooit weg van de Aarde.”
Het zou echter tot 1687 duren voordat Isac Newton in zijn gravitatiewet een formule beschreef die de aantrekking door de zwaartekracht tussen twee voorwerpen beschrijft. Maar terug naar het getal nul.
Het getal nul
De mensheid heeft het heel lang zonder het getal nul gedaan. Pas in 628 komt Brahmagupta met 0 als getal op de proppen. Daarvoor wordt het begrip nul niet als een getal maar alleen als een ‘plaatswijzer’ in positionele getallenstelsels gebruikt. Positionele getallenstelsels zijn getallenstelsels waar de positie van het cijfer in het getal mede de waarde bepaalt. De positie in het getal geeft aan of het bijvoorbeeld om een duizendtal, een honderdtal of een tiental gaat.
Als een bepaalde positionele waarde in een getal niet voorkomt – er zijn bijvoorbeeld geen tientallen – dan wordt op die plaats een nul gezet, de zogenaamde ‘plaatswijzer’ (ook wel “plaatsvervangende nul’ genoemd). Dit om de posities van de andere cijfers te behouden. Zo geeft de nul in het getal 201 aan dat er geen tientallen zijn, maar weten we door de aanwezigheid van die 0 wel dat de 2 in 201 staat voor 200. Soms kan men de plaatsvervangende nullen weg laten, vooral aan het einde van een getal, als de context duidelijk maakt wat wordt bedoeld. Als iemand bijvoorbeeld vraagt “wat kost dat huis?” en de ander antwoordt “375” dan zullen er weinig mensen zijn die denken dat het huis 375 euro kost in plaats van 375.000 euro.
Plaatswijzers in getallen is iets wat de oude Egyptenaren, de Babyloniërs en de Maya’s ook al kenden. Alleen gebruiken ze daarvoor niet het symbool 0. Zo maken de Babyloniërs in 450 voor Christus gebruik van lege plekken (spaties) om aan te geven dat een bepaalde positionele waarde in een getal niet voor komt. Op die positie is er “niets”; vandaar de lege plaats. Later gaan ze over op een teken dat nog het meest weg heeft van twee omvallende drankglazen. Andere culturen gebruiken cirkels, punten en allerlei kriebeltjes als plaatswijzers.
Vier voorbeelden van een plaatswijzer zoals deze in de oudheid wordt gebruikt. Van links naar rechts: De omvallende glazen van de Babyloniërs, een Chinese cirkel, een Indiaanse punt en het teken dat in de Mayo-cultuur als plaatswijzer wordt gebruikt.
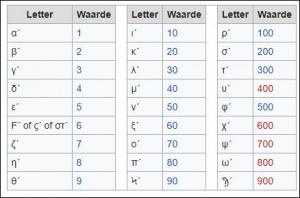
Naast positionele getallenstelsels zijn er ook andere getallenstelsels. Zo hanteren de oude Grieken een niet-positioneel getallenstelsel, gebaseerd op hun alfabet (elke letter heeft een bepaalde waarde). Ze hebben daarmee dan ook geen plaatsvervangende nul nodig. Een getal met de waarde 0 kennen ze niet.
De waarde van de Griekse letters.
Archimedes is de eerste Griek die van de alfabet-getallen afwijkt en met machten van tien op de proppen komt om zijn zogeheten zandgetal te kunnen berekenen. Hij bedenkt echter niet het getal ‘0’. De Grieken houden zich ook niet zo bezig met algebra, maar vooral met geometrie. Hun getaltheorie is dan ook gebaseerd op geometrische zaken zoals de lengte van lijnen en een lijn met een lengte 0 bestaat niet.
Vòòr Brahmagupta is er geen getal 0. Je hebt niets, niks, geen, leeg, enzovoorts, maar geen getal 0. Het idee van ‘0’ als getal lijkt o zo simpel, maar het vraagt om een andere manier van denken. Zo kan je niet tot nul tellen. Het is een stap die boven het tellen uitstijgt. Van “ik heb geen koeien” tot “Ik heb nul koeien”. Die stap hebben veel volken in de oudheid niet gemaakt. De eerste die met een definitie van het getal nul als getal op de proppen komt en er rekenregels voor opstelt, is in 628 de dan dertigjarige Brahmagupta.
Of hij daadwerkelijk echt de allereerste is, is niet zeker. Zo is daar het zogeheten ‘Bakhshali Manuscript’. Dit is een wiskundig document van meerdere pagina’s geschreven op berkenschors.
Een pagina uit het manuscript. Afbeelding Universiteit van Oxford.
Het is in 1881 gevonden in de buurt van Peshawar. Sinds 1902 bevindt zich het in de Universiteit van Oxford. Carbondateringstechniek laat zien dat de pagina’s van dit document dateren uit een periode die zo’n vijf eeuwen beslaat, van de derde tot de negende eeuw na Christus. Op sommige pagina’s is een punt te zien die als het getal nul gezien kan worden en waarvan het gebruik onduidelijk is. De “nul” zou dus ook al in de derde eeuw “uitgevonden” kunnen zijn, maar hoogst waarschijnlijk dient hij in dit manuscript alleen als plaatswijzer.
Brahmagupta is in ieder geval wel degene die als eerste uitgebreid het getal nul beschrijft en regels voor het rekenen met het getal 0 opstelt.
Wie is Brahmagupta?
Over de persoon Brahmagupta is erg weinig bekend. Hoe hij er bijvoorbeeld uitzag is niet bekend. Je ziet wel eens plaatjes van de man, maar die afbeeldingen zijn waarschijnlijk afkomstig uit iemands fantasie.
Twee totaal verschillende Brahmagupta ‘s
Brahmagupta is een Hindoe. Zijn vader zou iemand zijn met de naam Jisnugupta. Wanneer en waar Brahmagupta geboren is, weten we niet zeker, maar vermoedelijk is hij in het jaar 598 geboren in Bhillamala, tegenwoordig bekend onder de naam Bhinmal, een stad in het noordwesten van het huidige India. (Soms wordt ook wel eens Ujjain als zijn geboortestad genoemd.)
Bhillamala is in ieder geval de stad waar Brahmagupta het grootst gedeelte van zijn leven doorbrengt en waar hij zich bezig houdt met de wiskunde en astronomie. De stad is in die tijd de hoofdstad van het rijk van de Gurjara-dynastie. De stad kent een belangrijke wetenschappelijke school waar Brahmagupta werkt.
Het is in Bhillamala waar Brahmagupta het boek schrijft waarmee hij beroemd is geworden. In het boek definieert Brahmagupta het getal nul als de uitkomst die je krijgt als je van een getal hetzelfde getal aftrekt. Hij noemt deze uitkomst overigens geen ‘nul’, maar śūnya, een woord dat vandaag de dag nog steeds in India wordt gebruikt en dat niets betekent. (Om misverstanden te voorkomen, het betekent wel iets namelijk het woordje ‘niets’.)
In het boek geeft Brahmagupta rekenregels hoe je met het getal śūnya moet rekenen. Zo stelt hij (vrij vertaald) de volgende rekenregels op.
- Als je bij een getal X nul optelt, dan verandert dat getal niet; (X+0 = X)
- Als je van een getal X nul afhaalt, dan verandert dat getal niet; (X-0) = X)
- Nul plus nul is nul; (0+0 = 0)
- Nul minus nul is nul; (0-0 = 0)
- Als je een getal X met 0 vermenigvuldigt, dan bedraagt de uitkomst 0; (X*0 = 0)
- Als je een getal X door 0 deelt, dan bedraagt de uitkomst X/0; (Brahmagupta heeft geen oplossing voor deze berekening, hetgeen ook logisch is want delen door nul kan niet.)
- Als je nul deelt door nul, dan is de uitkomst 0; (0/0 = 0). Hier zit Brahmagupta fout. Delen door nul kan nooit, ook niet als de teller 0 is. Of zoals het ezelsbruggetje luidt: ‘Delen door nul is flauwekul’.
Brahmagupta geeft ook rekenregels hoe je met negatieve getallen moet omgaan. Hij noemt deze getallen overigens geen ‘negatieve getallen’, maar heeft het over ‘schulden’. Positieve getallen noemt hij ‘bezittingen’. Zo poneert hij het volgende over eventuele tekenwisselingen (van plus naar min e.d.) bij berekeningen:
- Een positief getal gedeeld door een positief getal geeft een positief getal
- Een negatief getal gedeeld door een negatief getal geeft een positief getal
- Een positief getal gedeeld door een negatief getal geeft een negatief getal
- Een negatief getal gedeeld door een positief getal geeft een negatief getal
- Een positief getal vermenigvuldigt met een positief getal geeft een positief getal
- Een positief getal vermenigvuldigt met een negatief getal geeft een negatief getal
- Een negatief getal vermenigvuldigt met een negatief getal geeft een positief getal
Vooral de regels “min gedeeld door min is plus” en “min maal min is plus” kunnen we als een doorbraak zien in het denken van hoe om te gaan met negatieve getallen. Het concept van negatieve getallen is overigens al langer bekend, zo kennen de oude Grieken ook negatieve getallen. Wel heeft men in de oudheid moeite met rekenen met negatieve getallen. Dit omdat men vooral in visuele eenheden denkt (“iemand heeft drie koeien; ik haal er vijf weg; hoeveel koeien heeft de man nog over?”). Zo schrijft bijvoorbeeld in de derde eeuw voor Christus de bekende Griekse wiskundige Diophantus in zijn boek ‘Arithmetica’ dat de vergelijking 4*X + 20 = 4 een absurde vergelijking is, dit omdat er geen oplossing is met een positief getal. Tegenwoordig zouden we gewoon zeggen: X = -4.
Brahmagupta is naast wiskundige vooral actief als astronoom. Hij is een tijd lang het hoofd van de sterrenwacht van Ujjain, een stad op zo’n 500 km afstand van Bhillamala. Hij schrijft tijdens zijn leven meer over astronomische zaken dan over wiskunde. Zo schrijft hij in één van zijn geschriften dat de Aarde rond is en een omtrek heeft van 36.000 km Daarmee schat hij de omtrek van de Aarde zo’n 10% te laag in; in werkelijkheid bedraagt de omtrek van de Aarde 40.075 km. Die 10% afwijking is een behoorlijke afwijking. Andere geleerden uit de oudheid schatten de omtrek van de Aarde aanmerkelijk beter in. Zijn inschatting van de duur van een zonnejaar is daarentegen wel opmerkelijk nauwkeurig. Hij stelt een zonnejaar gelijk aan 365 dagen, 6 uur en 5 minuten. Hier zit hij maar 16 minuten mis. (Een zonnejaar duurt 365 dagen, 5 uur en 49 minuten.)
In 670 overlijdt Brahmagupta op 72-jarige leeftijd. Maar met zijn overlijden verdwijnen niet zijn ideeën over het getal nul. Deze verspreiden zich langzaam maar zeker over de wereld, het eerst over China en Arabië. Richting Europa gaat het echter niet zo vlot. Pas vijf eeuwen later zien we de nul in Europa opduiken met de introductie van de Indisch-Arabische getallennotatie in Europa.
Degene die de nul in Europa introduceert is in 1202 Leonardo van Pisa, beter bekend als Fibonacci. De Europeanen hebben aanvankelijk wel wat moeite met het getal 0. Zo verbiedt in 1299 het stadbestuur van Florence zelfs het gebruik van het cijfer 0. Ze vinden het cijfer 0 niet alleen fraudegevoelig – je kan een 0 zo in een 9 veranderen – maar nul is ook de poort naar de negatieve getallen en negatieve getallen staan voor schulden en schulden zijn slecht. Gelukkig vind de maatregel van het stadsbestuur van Florence geen navolging, want anders hadden we vandaag de dag geen computers gehad.
Voor wat betreft de ontwikkeling van de naam van het getal nul, de Arabieren noemen de nul eerst ‘sifr’ (leeg); later wordt dat ‘safira’ dat net zoals het Indiaanse woord śūnya ‘niets’ betekent. In Italië wordt dat ‘safira’ door Fibonacci vertaald als ‘zephyrum’, later verkort tot ‘zefiro’. Wiskundigen in Venetië korten dat vervolgens nog een keer in tot ‘zero’, welk woord ook door de Fransen en de Engelsen wordt overgenomen.
Tot slot, er wordt wel eens gezegd dat iets van nul en generlei waarde is, waarmee wordt aangegeven dat iets niets waard is, maar dat geldt beslist niet voor Brahmagupta’s ideeën over het getal nul. Zijn nul is de basis van de moderne wiskunde, waarmee overigens niet wordt gezegd dat de wiskunde op “niets” is gebaseerd. En voor Brahmagupta geldt: van zero tot hero.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie