Het is voor de mensheid maar goed dat niet alle berekeningen van de Schotse wiskundige John Napier klopten. Was dat wel het geval geweest, dan hadden we niet meer bestaan, want volgens berekeningen van Napier, gemaakt in 1593 en gebaseerd op theologische geschriften, zou de wereld in 1688 vergaan, en als het niet in dat jaar gebeurde, dan zou de dag des oordeels in 1700 plaats vinden. Het kan natuurlijk ook zijn dat zijn berekeningen wel klopten, maar dat zijn uitgangspunten onjuist waren.
Omdat de voorspellingen van John Napier niet klopten, kon in 1835 Samuel Freeman dit portret van hem schilderijen. Het is gebaseerd op een oud schilderij van Napier uit 1616.
John Napier is in de wiskunde een beroemde naam. Hij geldt als de bedenker van de logaritme. In 1614 verschijnt zijn boek ‘Mirifici Logarithmorum Canonis Descriptio’, waarin hij het concept van logaritmes beschrijft. Dit is echter niet de enige reden dat hij is opgenomen in het overzicht van de mensen achter de computer. Dat heeft hij ook te danken aan zijn zogenaamde ‘Napier’s Bones’ (in het Nederlands ook wel de ‘beenderen van Napier genoemd’). Het zijn ivoren staafjes waarop getallen staan. De staafjes kan men gebruiken als hulpmiddel bij het maken van vermenigvuldigen en delingen. Het is gebaseerd op een “idee” dat al in het oude India en Egypte bekend was.
Een setje van Napier’s bones uit de zeventiende eeuw; Landesmuseum Baden-Württemberg, Stuttgart; foto Dr. Bernd Gross.
Wie is John Napier
Jhone Neper, zoals Napier in zijn tijd bekend staat – er deden in die tijd meerdere variaties van zijn naam de ronde maar niet de versie (John Napier) waaronder wij hem nu kennen – is de oudste zoon van een grootgrondbezitter in Schotland. Zijn vader, Sir Archibald Napier of Merchiston Castle – om misverstanden te voorkomen, hier wordt niet bedoeld dat het onbekend is of Sir Archibald Napier zijn vader is of dat dit Merchiston Castle is; het betreft hier het Engelse woordje ‘of’ – trouwt als vijftienjarige in 1549 met de eveneens vijftienjarige Janet Bothwell, de oudste dochter van een andere Schotse grootgrondbezitter. In die tijd wordt in die kringen vaak op jonge leeftijd gehuwd.
Een jaar later wordt John geboren. Over zijn jeugd is weinig bekend. Hij gaat niet naar school maar krijgt net zoals veel andere kinderen van rijke ouders thuis privéonderwijs van zogeheten tutoren. Er is een brief bewaard gebleven van een oom, de bisschop van Orkney, gericht aan zijn vader, waarin hij hem dringend adviseert om de op dat moment elfjarige John naar Frankrijk of Vlaanderen te sturen om daar zijn opleiding voor te laten zetten. “Ik bid u om uw zoon Jhone naar school te sturen; naar Frankrijk of Vlaanderen; want hij kan hier niet goed leren en geen winst behalen in deze meest gevaarlijke wereld…”
Of hij dat inderdaad gedaan heeft, is niet bekend. Wel is bekend dat in 1563 de dan 13-jarige John Napier zijn entree maakt aan St Andrews, de bekendste en oudste universiteit in Schotland. Hij staat daar ingeschreven onder de naam Johannes Neaper. Naar verluidt zou de jonge Napier vooral in theologie geïnteresseerd zijn, iets wat hem zijn hele leven bezig zal houden.
Hij studeert er niet af – zijn naam ontbreekt in de boeken met namen van mensen die er afstuderen – maar zou voor zijn verdere opleiding naar het vasteland van Europa zijn vertrokken. Naar verluidt heeft hij aan de universiteit van Parijs gestudeerd, maar ook landen als Nederland, Zwitserland en Italië worden genoemd als landen waar hij zijn opleiding verder heeft genoten. Vermoedelijk doet hij dit om er beter Latijn en Grieks te leren, de talen van de oudheid en wetenschap. Vooral om Grieks te leren kan je beter op het continent zijn dan in Schotland. In ieder geval beheerst hij, als hij in 1571 op 21-jarige leeftijd terug keert in Schotland, deze talen. Ook heeft hij een grote interesse in de wiskunde en astronomie ontwikkeld.
Portret van Napier, gemaakt door een zekere mr. Brown; jaartal onbekend; bron: ‘Wellcome Library, London” en een portret van Elizabeth Stirling, de eerste mevrouw Napier
In 1572 neemt hij het beheer van de landgoederen van zijn vader over. Hetzelfde jaar trouwt hij met Elizabeth Sterling, dochter van een Schotse grootgrondbezitter. Het is een gearrangeerd huwelijk. Elizabeth brengt het grootste gedeelte van het landgoed van haar vader in. Haar vader, James Stirling, staat bekend als een wiskundige, iets wat Napier aangesproken zal hebben. Napier en zijn vrouw krijgen vier kinderen. Nadat zijn vrouw in 1579 overlijdt, hertrouwt hij met Agnes Chisholm, eveneens een dochter van een grootgrondbezitter. Met haar krijgt hij ook nog eens tien kinderen (en belangrijk, ook een stuk grond erbij).
Naast het beheren van de landgoederen – in 1574 laat hij een nieuw kasteel bouwen op zijn nieuw verkregen land – houdt hij zich aanvankelijk vooral bezig met godsdienstzaken. Hij is een fanatiek aanhanger en verdediger van het protestantisme. Als de Spaanse armada van de katholieke Spaanse koning Philips II in de zomer van 1588 naar Engeland vaart, stelt Napier voor om met hulp van de zon en grote brandpuntspiegels de houten Spaanse schepen in brand te steken. Een idee dat hij heeft opgepikt uit oude Griekse verhalen. De Engelse admiraliteit vertrouwt echter meer op haar eigen schepen dan op de aanwezigheid van een zonnetje en de armada wordt zonder brandspiegels verslagen.
Het zal niet het enige militaire idee van Napier zijn dat hij bedenkt en dat niet wordt uitgevoerd. In 1596 publiceert hij een schrijven getiteld: ‘Secret inventions, profitable and necessary in these days for defence of this island’. Hij komt onder andere met een soort tank op de proppen – de mensen die er in zitten, moeten het voertuig als een soort Fred Flinstone-auto voortbewegen – en iets wat je als een onderzeeboot kan zien. Privé houdt Napier zich bezig met het zoeken naar manieren om de opbrengst van zijn landgoed te verbeteren. Zo experimenteert hij met meststoffen en het strooien van zout om de grond van zijn land te verrijken.
In 1593 publiceert hij een godsdienstig boek getiteld ‘A Plaine Discovery of the Whole Revelation of Saint John’. Hierin gaat hij fel te keer tegen het katholicisme. Zo beweert hij dat de op dat moment regerende paus de antichrist is. Het is ook dit boek waarin hij zijn voorspelling van de dag des oordeels doet. Die dag zal in 1688 of in 1700 komen, althans zo leerden berekeningen hem – blijkbaar waren er twee oplossingen mogelijk. Het boek is een groot succes en het wordt ook in het Nederlands, Duits en Frans vertaald. Napier dacht zelf altijd dat als hij later in de geschiedenisboeken zou belanden, het dit dankzij dit boek zou zijn.
Links, het kaft van een eerste druk uit 1593. Het boek bracht in 2019 op een veiling 1300 pond op; Rechts de pagina waarin hij voorspelt dat de wereld in 1688 of in 1700 zal vergaan.
Nadat Napier zijn godsdienstige boek heeft gepubliceerd, gaat hij zich meer met de wiskunde en de astronomie bezig houden. Eén van de grote problemen waar de wiskunde op dat moment mee zit, is het rekenen met grote getallen. In het voorwoord van een wiskundeboek uit 1614 schrijft Napier hierover:
“Aangezien er niets is, geliefde studenten van de wiskunde, dat zo lastig is voor de wiskundige praktijk, en dat het rekenen meer lastig maakt en hindert dan de vermenigvuldigingen, delingen, vierkante en kubusvormige extracties van grote getallen, die naast de vervelende kosten van de benodigde tijd grotendeels onderhevig zijn aan vele glibberige fouten, begon ik daarom in mijn geest te overwegen met welke zekere en gemakkelijke kunst ik die hindernissen zou kunnen verwijderen.”
Napier bedenkt dat je makkelijker met grote getallen kan rekenen als je de grote getallen gaat zien als machten van kleinere getallen. Zo is bijvoorbeeld het getal 729 gelijk aan 3 tot de macht 5 (ter controle: 3 x 3 x 3 x 3 x 3 = 729; het klopt). Napier komt nu met een wiskundig idee op de proppen – hij noemt het ‘logaritme – dat je als hulpmiddel kan gebruiken om te kunnen rekenen met grote getallen.
De logaritme van een getal X definieert hij als de exponent waarmee een waarde, het zogenaamde grondtal, moet worden verheven om het getal X als resultaat te verkrijgen. Wat wetenschappelijker geformuleerd wordt de logaritmische functie – meestal afgekort tot ‘log’ – gedefinieerd als de inverse van een exponentiële functie. Dit klinkt wat ingewikkeld, daarom een voorbeeld.
Stel, we kiezen als grondtal het getal 10, dan is bijvoorbeeld de logaritme van het getal 100 met het grondtal 10 het getal 2, immers 10 tot de macht 2 is 100; (10 x 10 = 100). Idem is de logaritme voor het getal 1000 met het grondtal 10 gelijk aan 3, want 10 tot de macht 3 is 1000; (ter controle: 10 x 10 x 10 = 1000; dit had u ook gekund).
Omdat wiskundig gezien – vraag niet hoe het kan, maar profiteer er van – de volgende stellingen gelden log (A x B) = log (A) + log (B) en log (A : B) = log (A) – log (B), kan je met behulp van logaritmische functies lastige vermenigvuldigingen en delingen uitrekenen met behulp van het simpelere optellen en aftrekken. Wel heb je hiervoor een boek met logaritmetabellen nodig, de zogenaamde logaritmetafels. Dat zijn boeken met eindeloze reeksen getallen en hun bijbehorende logaritmes.
Een voorbeeldje om te laten zien hoe je met logaritmes kan rekenen: stel we willen uitrekenen hoeveel 100 x 1000 is. Niet echt een vermenigvuldiging waarvoor je gebruik zou hoeven te maken van logaritmes, maar goed, stel dat we dit wel met behulp van logaritmes willen uitrekenen.
We zagen zonet al dat log (100) = 2 en dat log (1000) = 3. Nu maken we gebruik van de formule log (A x B) = log (A) + log (B). Oftewel in dit geval log (100 * 1000) = log (100) + log (1000) = 2 + 3 = 5. Vervolgens zoeken we in het grote boek – niet dat van Sinterklaas maar het boek met de logaritmetabellen op voor welk getal X geldt dat log (X) = 5. Dat blijkt het getal X = 100.000 te zijn. Oftewel de uitkomst van 100 x 1000 is 100.000.
Nu is 100 x 1000 uiteraard een vermenigvuldiging die we ook heel goed zonder de hulp van logaritmes kunnen maken, maar bij vermenigvuldigingen van minder mooie grote getallen zijn logaritmes, zeker in de tijd dat er geen rekenmachines bestaan, een handig hulpmiddel. Zo maken bijvoorbeeld alle rekenlinialen gebruik van logaritmes.
Logaritmes worden ook vaak gebruikt om met behulp van schalen verhoudingen aan te geven. Bij sommige zaken gaat het namelijk niet zo zeer om de absolute waarde maar meer om de (logaritmische) verhouding ten opzichte van een basiseenheid. Bekende logaritmische schalen zijn de decibel-schaal voor het geluidsniveau en de schaal van Richter voor de sterkte van aardbevingen.
Zo geeft een aardbeving met een kracht van 4 op de schaal van Richter een tien keer zo grote magnitude uitslag als een aardbeving met een kracht van 3 op de schaal van Richter en een aardbeving met een kracht van 5 een honderd keer zo’n grote magnitude-uitslag als die van eentje met schaal 3, enzovoorts, enzovoorts.
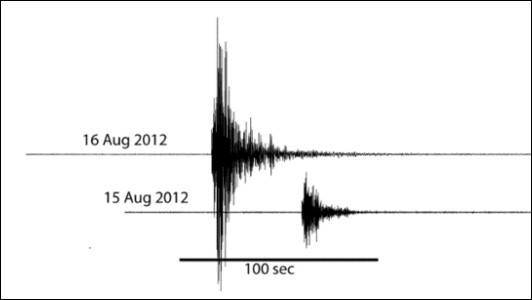 De seismogrammen van twee aardbevingen. Die van 15 augustus 2012 vond plaats bij Leermens in de provincie Groningen en had een kracht van 2,4 op de schaal van Richter. Een dag later was er een aardbeving bij Huizinge. Die had een kracht van 3,6 op de schaal van Richter met een ruim tien keer zo grote uitslag.
De seismogrammen van twee aardbevingen. Die van 15 augustus 2012 vond plaats bij Leermens in de provincie Groningen en had een kracht van 2,4 op de schaal van Richter. Een dag later was er een aardbeving bij Huizinge. Die had een kracht van 3,6 op de schaal van Richter met een ruim tien keer zo grote uitslag.
In 1614 publiceert Napier zijn boek ‘Mirifici logarithmorum canonis descriptio’, waarin hij een beschrijving geeft van zijn idee van logaritmes. Het woord logaritme is een samentrekking van de Griekse woorden; logos (rede) en arithmos (getal). Ongeveer tegelijkertijd, en misschien zelfs wel eerder, bedenkt de Zwitserse klokkenmaker Jost Bürgi ook het concept van de logaritme maar hij publiceert hier pas in 1620 een schrijven over, waardoor John Napier te boek staat als de bedenker van de logaritme.
Napier gebruikt bij de logaritmes in zijn boek overigens niet het grondtal 10. Zijn oorspronkelijke invalshoek is meer meetkundig dan algebraïsch. Henry Briggs, een Engelse wiskundige leest het boek en is diep onder de indruk. Hij reist naar Schotland en overtuigt Napier om met het grondgetal 10 te gaan werken. Napier vindt het een goed idee. Briggs gaat daarop aan het werk en berekent voor alle gehele getallen tussen de 1 en 1000 de logaritme met het grondgetal 10.
In 1616 verschijnt een Engelse editie van Napier’s boek met daarin een extra hoofdstuk met een tabel van de logaritmes van deze 1000 getallen. In 1624 publiceert Briggs een eigen boek met daarin voor het grondtal 10 alle logaritmes van de gehele getallen tussen 0 en 20.000, plus de logaritmes voor de gehele getallen tussen 90.000 en 100.000.
Het boek van Briggs en een pagina uit dit boek met de logaritmes voor de eerste 34 getallen (met 14 cijfers achter de komma).
Opvallenderwijs slaat Briggs de getallen tussen 20.000 en 90.000 over. Deze leemte wordt in 1626 ingevuld door de Nederlandse landmeter Ezechiel de Decker die voor alle getallen van 1 tot 100.000 de logaritme uitrekent. Napier maakt het uitkomen van al deze tabellenboeken echter niet mee. Hij overlijdt op 4 april 1617 op 67-jarige leeftijd.
John Napier in 1616, een jaar voor zijn dood
Wat Napier ook net niet meemaakt, is de uitgifte van zijn boek ‘Rabdologiae’. Dit verschijnt enige maanden na zijn overlijden. Het is dit boek waarin Napier zijn rekenstaafjes beschrijft, waaraan hij mede zijn plaats in de mensen achter de computer te danken heeft. Zijn rekenstaafjes zijn een hulpmiddel om te kunnen vermenigvuldigen en delen. Ze hebben niks met logaritmes te maken, maar maken gebruikt van een methode die al eeuwenlang in oude beschavingen in Azië en in Arabië wordt gebruikt om te kunnen vermenigvuldigen.
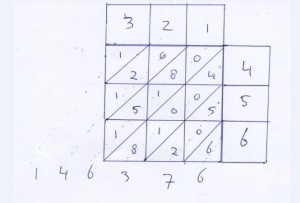
Het werkt als volgt. Stel we willen de getallen 321 en 456 met elkaar vermenigvuldigen. Nu kunt u een rekenmachine pakken of de berekening uit het hoofd doen – ik schat mijn lezers hoog in – en dan zal u zien dat uitkomsten van 321 x 456 gelijk is aan 146.376. Zelf heb ik er wel even een kladblaadje bij gepakt en dan kom ik ook tot deze uitkomst van 146.376.
Nu kan je deze berekening op papier ook op een ander manier maken. In het oude India en Egypte deed men het vaak zo.
Bovenaan schrijft men het te vermenigvuldigen getal (321) en helemaal rechts het getal (456) waarmee men het wil vermenigvuldigen. Vervolgens vermenigvuldig je alle deelcijfers van de getallen afzonderlijk met elkaar en schrijf je de uitkomsten daarvan in de hokjes er onder. Zie het voorbeeld. Wel moet je deze uitkomsten “diagonaal” opschrijven (zie bijvoorbeeld de uitkomst van 3 x 4 = 12 in het hokje onder de drie). Als de uitkomst van de vermenigvuldiging kleiner is dan 10, dan voeg je een ‘voorloop nul’ toe, bijvoorbeeld 2 x 4 = 8; dan schrijf je niet 8 maar 08. (zie bijvoorbeeld het vakje onder de ‘2’).
Vervolgens tel je de uitkomsten van de schuine lijnen (de diagonalen) op – je begint rechts – en schrijft de uitkomst van deze optelling onder de tabel (van rechts naar links). In het voorbeeld geeft de eerste diagonaal een 6. De volgende diagonaal levert de optelling 5+0+2=7 op; dan volgt 4+0+0+1+8=13. Deze uitkomst is groter dan 9. Als het resultaat van de optelling groter is dan 9, dan schrijf je alleen het rechtergetal van de uitkomst op (in dit geval dus de 3) en telt je het andere cijfer (in dit geval de 1) op bij de volgende sommatie. Dat geeft dan: 1+0+8+1+5+1=16 (6 opschrijven en 1 onthouden) en op dezelfde manier vind je ook nog achtereenvolgens een 4 en een 1. Onder de tabel verschijnt nu de uitkomst van de berekening en zie je dat 321*456 gelijk is aan 146.376.
Het nu even geniale als simpele idee van Napier – hoe moeilijk kan het zijn – was nu om de vermenigvuldigingen van alle deelcijfers al vast standaard klaar te hebben staan op ivoren staafjes met daarin de uitkomsten al diagonaal weergegeven. Je hoeft ze dan niet meer uit te rekenen (dat valt overigens wel mee) maar belangrijker, niet meer op te schrijven. Je hoeft alleen maar de goede staafjes te pakken en deze naast elkaar te leggen.
 Een doos met ‘Napier’s Bones’ uit 1650 zoals te zien is in het National Museum of Scotland; foto Kim Traynor; Wikipedia
Een doos met ‘Napier’s Bones’ uit 1650 zoals te zien is in het National Museum of Scotland; foto Kim Traynor; Wikipedia
Behalve voor vermenigvuldigingen kan je de staafjes ook gebruiken voor delingen en worteltrekken.
Tot slot, ten aanzien van Napier’s betekenis voor de wiskunde is er nog één puntje de moeite waard om hier te vermelden en wel de decimale punt. Het is John Napier die in 1617 voor het symbool “.” pleit om de “cijfers achter de komma” te scheiden van “de cijfers voor de komma”. En daarmee zijn we aan de laatste punt van zijn portret gekomen.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie