Wie ’s avonds (op het noordelijk halfrond) naar de sterrenhemel kijkt en een foto met een heel lange sluitertijd maakt, zou dit als resultaat kunnen zien.
 De sterren lijken een rondje aan de hemel te draaien. (Foto d.d. 1 december 2006 gemaakt door Steve Ryan; Groveland, CA, USA; bron Flickr.)
De sterren lijken een rondje aan de hemel te draaien. (Foto d.d. 1 december 2006 gemaakt door Steve Ryan; Groveland, CA, USA; bron Flickr.)
Nu zijn er twee verklaringen mogelijk voor dit fenomeen. De eerste verklaring luidt dat de aarde stil staat en de sterren ’s nachts een rondje om de aarde heen draaien. Deze theorie heeft eeuwenlang opgeld gedaan. De Indiaanse astronoom en wiskundige Aryabhata stelde echter dat je dit optische effect ook krijgt als de sterren ‘stil staan’ en het de aarde is die om haar eigen as draait. Uiteraard beschikte Aryabhata niet over een sterrenfoto maar wel over tekeningen van de bewegingen van de sterren die de oude Indiaanse astronomen met veel geduld hebben gemaakt.
Aryabhata is niet de eerste die veronderstelt dat het de aarde is die draait en niet de sterren – de oude Grieken hebben dit vermoeden al eerder geuit – maar hij is wel de eerste belangrijke astronoom die deze veronderstelling in een boekwerk opschrijft. Hij doet dat in het jaar 499 in zijn ‘Aryabhatiya’. Dit werk bevat 121 sutra’s (verzen) op het gebied van astronomie en wiskunde. Over de ‘relativiteit van bewegende sterren’ als gevolg van het draaien van de aarde schrijft hij: “Net zoals iemand in een boot die voorwaarts drijft, de zaken op de oever naar achteren ziet verdwijnen, zo ziet de mens de stationaire sterren bewegen terwijl het in werkelijkheid de aarde is die draait.”
Aryabhata schrijft ook dat de aarde in 23 uur 56 minuten en 4,10 seconden rondom zijn as draait. Gezien de 23 uur 56 minuten en 4,09 seconden waar men tegenwoordig vanuit gaat, is dat een verbluffend nauwkeurige inschatting. Ook berekent hij vrij nauwkeurig de omtrek van de aarde. Opvallend is dat na zijn dood – als zijn boek wordt ‘herdrukt’ – iemand de tekst over het draaien van de aarde aanpast. Aryabhata heeft ongetwijfeld een fout gemaakt, denkt deze persoon. In diens uitgave draaien de sterren weer gewoon om de stilstaande aarde heen.
Nog even iets over de foto van de ‘draaiende sterren’. Op de foto is één ster te zien die ‘niet beweegt’, maar in het middelpunt van de cirkel stil lijkt te staan. Die ster is de Poolster. Dat hij niet ‘draait’ komt omdat hij bijna precies in het verlengde van de denkbeeldige rotatie-as van de aarde staat. Dat de Poolster daardoor altijd op dezelfde plek (in het noorden) staat, is handig voor zeelui die willen weten waar ze zich op zee bevinden. Met hulp van de poolster kunnen ze hun breedtegraad op zee bepalen. De hoek aan de hemel waarop een waarnemer de Poolster ziet, is namelijk gelijk is aan de breedtegraad waarop de waarnemer zich bevindt. Door de hoek te meten, weet men aldus op welke breedtegraad het schip vaart. (De uitdrukking “poolshoogte nemen” vindt hier zijn oorsprong in.)
Historisch apparaat om de Poolshoogte mee te meten; CC0 – Pixabay – Marynistyka_Group)
Maar goed, terug naar Aryabhata. Hij is geboren in 476 na Christus. Dat weten we omdat hij in 499, als zijn boekwerk ‘Aryabhatiya’ verschijnt, opschrijft dat hij op dat moment 23 jaar oud is. Als zijn geboorteplaats wordt meestal Kusumapura vermeld – het huidige Patna, een stad met momenteel meer dan 2 miljoen inwoners. De stad ligt vlakbij de Ganges in het oosten van India.
De rode stip is Patna, het vroegere Kusumapura
Volgens sommige bronnen is Aryabhata echter in Ashmaka in het zuiden van India geboren, en weer andere bronnen hebben het over een stad in het noorden. We houden het er maar op dat hij ergens in het huidige India is geboren. Wel zijn de meeste bronnen het er over eens dat hij in ieder geval lange tijd gewoond en gewerkt heeft in Kusumapura.
Aryabhata is in de eerste plaats astronoom. Zijn wiskundige analyses dienen slechts om berekeningen op het gebied van de astronomie te kunnen maken. Als astronoom is Aryabhata baanbrekend. Niet alleen schrijft hij dat het de aarde is die om haar as draait, ook stelt hij dat niet alleen de maan maar ook de planeten alleen zichtbaar zijn omdat ze zonlicht weerkaatsen. Ook laat hij zien hoe zons– en maansverduisteringen tot stand komen. Wel gaat hij er ten onrechte van uit dat de aarde het middelpunt van het heelal is en dat de zon om de aarde draait.
Hij maakt ook berekeningen over de banen van de planeten, waarbij hij constateert – het is een juiste constatering – dat ze elliptisch van aard zijn. Om deze banen te kunnen berekenen moet hij oplossingen bedenken voor een aantal zogeheten diofantische vergelijkingen. (Diophantus van Alexandrië, die voor het eerst over dit soort vergelijkingen schrijft, is een Griekse wiskundige die leefde in de derde eeuw voor Christus.)
Een voorbeeld van een diofantische vergelijking is xn + yn = zn. Eén vergelijking met drie onbekenden (x, y en z). Voor n=1 en voor n =2 zijn er veel oplossingen mogelijk, maar voor n=3 en hoger bestaan er voor deze vergelijking geen oplossingen met natuurlijke getallen ongelijk aan 0. (Dit staat bekend als de beroemde laatste stelling van Fermat.)
Aryabhata houdt zich ook bezig met vlakke meetkunde, bolmeetkunde en goniometrie. Ook maakt hij allerlei berekeningen om kalenders te kunnen maken. Het probleem dat hij ondervindt bij het maken van zijn berekeningen is het op dat moment in gebruik zijnde Indiaanse getallenstelsel. Hij bedenkt daarom een praktischer getallenstelsel waarmee je gemakkelijker kan rekenen
Het is dit getallenstelsel dat Aryabhata een plek heeft gegeven in het overzicht van mensen achter de computer. Hij baseert zijn getallenstelsel op het Indiaanse alfabet uit die tijd. De eerste 25 medeklinkers gebruikt hij om de getallen 1 t/m 25 aan te geven. De andere acht medeklinkers staan voor de tientallen 30 t/m 100. De negen klinkers dienen om machten van het getal tien aan te geven. (Overigens bedenkt Archimedes, wie anders, in de derde eeuw voor Christus ook een systeem van getallen die bestaan uit machten van het getal tien.)
Het vernieuwende van het getallenstelsel van Aryabhata zit hem vooral in het combineren van ‘gewone getallen’ met getallen die bestaan uit machten van tien. Door deze te combineren met de ‘gewone getallen’ kan hij alle gehele getallen van 1 tot en met 10 18 vormen. Wel is het zo dat sommige getallen op meerdere manieren uit de ‘basisgetallen’ gevormd kunnen worden.
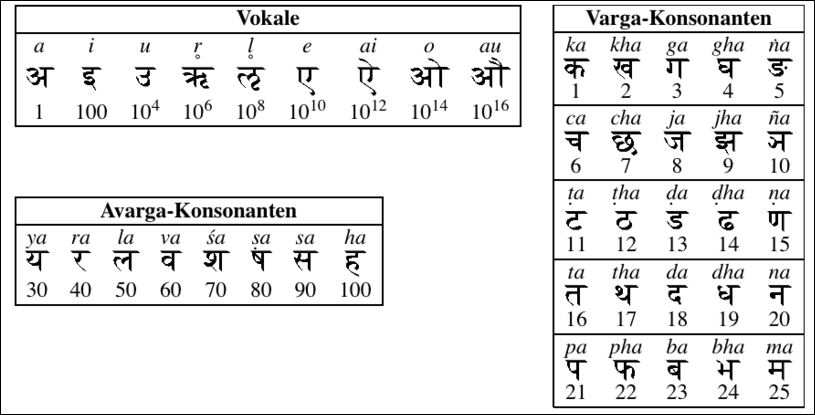 Zie hier zijn vertaling van de klinkers en medeklinkers in getallen; rechts staan de getallen 1 tot en met 25; linksonder 30 t/m 100 en linksboven de machten van 10; Bron Wikipedia
Zie hier zijn vertaling van de klinkers en medeklinkers in getallen; rechts staan de getallen 1 tot en met 25; linksonder 30 t/m 100 en linksboven de machten van 10; Bron Wikipedia
Met zijn stelsel is het veel gemakkelijk rekenen dan bijvoorbeeld met het Romeinse getallenstelsel dat op dat moment in Europa het gangbare getallenstelsel is. In zijn boek ‘Aryabhatiya’ staat een voorbeeld van een opvallende berekening waarbij hij gebruik maakt van zijn nieuwe grote getallen: “Caturadhikaṃ śatamaṣṭaguṇaṃ dvāṣaṣṭistathā sahasrāṇām ayutadvayaviṣkambhasyāsanno vṛttapariṇāhaḥ”.
Voor wie wat minder goed zijn talen spreekt dan uw schrijver, hierboven staat: “Tel vier op bij honderd, vermenigvuldig dit met acht, en telt er dan 62.000 bij op, dan kan krijgt men een benadering van de omtrek van een cirkel met een diameter van 20.000.” (In de tijd van Aryabhata wordt nog niet gebruik gemaakt van formules in een wiskundige notatie met tekens als ”+, –, x en /” maar schrijft men de formule gewoon taalkundig helemaal als tekst uit.)
Voor wie denkt “waar slaat deze berekening op?” het is een berekening waarin een benadering van het getal pi “verstopt” zit. Als we de berekening met de getallen van Aryabhata uitvoeren, dan zien we: ((4 + 100) × 8 + 62.000) / 20.000 = 62.832 / 20.000 = 3,1416 en dat getal is een behoorlijk goede benadering van pi. Zeker voor die tijd. Waar deze ‘formule’ vandaan komt vermeldt Aryabhata niet. Dat geldt ook voor een aantal andere wiskundige stellingen in zijn werk. Ook daar geeft hij geen enkel bewijs voor, maar waarschijnlijk geeft Aryabhata geen bewijzen, omdat de wiskunde voor Aryabhata slechts een ondersteuning is voor zijn astronomiewerk.
Sommige historici stellen dat Aryabhata ook al het concept nul kent, met ‘nul’ dan in de hoedanigheid als het getal 0, maar daar is geen bewijs voor. Het is zijn landgenoot Brahmagupta die voortbouwend op het getallengestel van Aryabhata ruim honderd jaar later als eerste met het getal “nul” op de proppen komt.
Naast de ‘Aryabhatiya’ heeft Aryabhata in ieder geval nog twee andere (en wellicht nog meer) boekwerken geschreven. Deze zijn echter allemaal verloren gegaan. Zo schrijft zijn tijd- en landgenoot Varāhamihira over een boek van Aryabhata, dat getiteld ‘Arya-siddhanta’ zou zijn, en waarin niet alleen allerlei astronomische berekeningen zouden staan maar waarin ook diverse astronomische meetinstrumenten worden beschreven. Ook wordt in een Arabisch wiskundig boek uit de negende eeuw een onbekend boekwerk van Aryabhata vermeld.
Over de persoon Aryabhata zelf is verder weinig bekend. Hij zou in de tijd van het Gupta-dynastie als astronoom gewerkt hebben aan de boeddhistische universiteit van Nalanda in Patna, maar of dat klopt is niet zeker. Aryabhata was geen boeddhist maar een hindoe. Behalve zijn geboortejaar weten we verder eigenlijk alleen nog dat hij in het jaar 550 op 73-jarige leeftijd is overleden. Dat is dus vijftig jaar nadat hij als 23-jarige zijn meesterwerk schreef. Vooral In India wordt hij vandaag de dag nog zeer vereerd. Zo droeg de eerste Indiaanse satelliet, gelanceerd in 1975, zijn naam. Ook is een krater op de maan naar hem genoemd.
Naar het volgende verhaal uit deze serie.
Naar het vorige verhaal uit deze serie